Операции над событиями
В теории вероятностей существуют ровно те же операции над множествами, что и в теории множеств.
Определение 4.
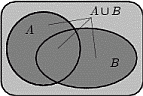
1. Объединением 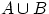 событий
событий 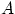 и
и 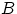 называется событие, состоящее в том, что произошло либо
называется событие, состоящее в том, что произошло либо 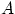 , либо
, либо 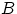 , либо оба события одновременно. На языке теории множеств
, либо оба события одновременно. На языке теории множеств 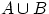 есть множество, содержащее как элементарные исходы из множества
есть множество, содержащее как элементарные исходы из множества 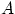 , так и элементарные исходы из множества
, так и элементарные исходы из множества 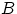 .
.
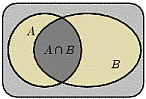
2. Пересечением 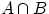 событий
событий 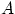 и
и 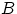 называется событие, состоящее в том, что произошли оба события
называется событие, состоящее в том, что произошли оба события 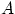 и
и 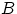 одновременно. На языке теории множеств
одновременно. На языке теории множеств 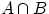 есть множество, содержащее элементарные исходы, входящие в пересечение множеств
есть множество, содержащее элементарные исходы, входящие в пересечение множеств 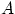 и
и 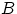 .
.
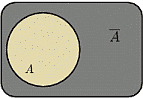
3. Противоположным (или дополнительным) к событию 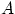 называется событие
называется событие 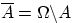 , состоящее в том, что событие
, состоящее в том, что событие 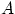 в результате эксперимента не произошло. Т.е. множество
в результате эксперимента не произошло. Т.е. множество 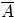 состоит из элементарных исходов, не входящих в
состоит из элементарных исходов, не входящих в 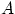 .
.
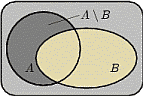
4. Дополнением 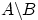 события
события 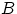 до
до 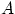 называется событие, состоящее в том, что произошло событие
называется событие, состоящее в том, что произошло событие 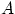 , но не произошло
, но не произошло 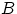 . Т.е. множество
. Т.е. множество 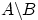 содержит элементарные исходы, входящие в множество
содержит элементарные исходы, входящие в множество 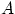 , но не входящие в
, но не входящие в 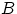 .
.
Определение 5.
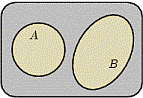
1. События 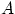 и
и 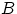 называют несовместными, если
называют несовместными, если 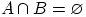 .
.
2. События 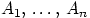 называют попарно несовместными, если для любых
называют попарно несовместными, если для любых 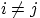 , где
, где 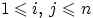 , события
, события 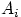 и
и 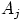 несовместны.
несовместны.
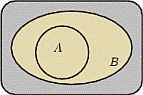
3. Говорят, что событие 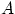 влечёт событие
влечёт событие 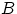 , и пишут
, и пишут 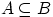 , если всегда, как только происходит событие
, если всегда, как только происходит событие 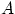 , происходит и событие
, происходит и событие 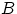 . На языке теории множеств это означает, что любой элементарный исход, входящий в множество
. На языке теории множеств это означает, что любой элементарный исход, входящий в множество 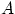 , одновременно входит и в множество
, одновременно входит и в множество 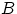 , т.е.
, т.е. 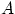 содержится в
содержится в 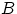 .
.
Дата добавления: 2020-04-12; просмотров: 708;











