Самостоятельная работа.


Предлагаю вам проделать самостоятельные рассчеты, построения и обработку графиков в следующей виртуальной лабораторной работе под кодовым названием "Определить жесткость пружины". Но поднимем планку Эксперимента на более высокий уровень: надо не просто получить число, но сравнить два метода измерения жесткости пружины – статический и динамический.

Кратко рассмотрим эти методы.

Статический метод.

Если подвесить к закрепленной вертикальной пружине груз массой 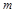, то пружина растянется на 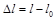согласно закону Гука, где 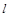– длина растянутой пружины, а 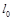– длина нерастянутой пружины (начальная длина).

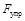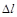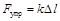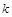Примечание: закон Гука говорит о пропорциональности силы упругости пружины абсолютному удлинению , т.е. , где – коэффициент упругости (или жесткость) пружины.

В состоянии равновесия сила тяжести груза уравновесится силой упругости и мы можем написать 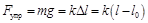. Раскроем скобки и увидим зависимость длины пружины от массы груза

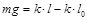
Если сделать замену переменных 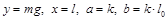, то получится уравнение прямой 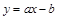. Не надо делать линеаризацию!

Итак, перед вами стоит задача обработать данные из таблицы 10, которые были занесены туда юным Экспериментатором (ему надоело бросать кирпичи с крыши девятиэтажного дома). Для опытов он запасся набором грузов, нашел десяток-другой разных пружин и, подвешивая грузы разных масс, замерял длину растянутой пружины с помощью миллиметровой линейки.

 

Задание 1.

1. Выберите номер пружины из таблицы 10.

2. Составьте свою таблицу из двух столбцов. В первый столбец занесите силу тяжести 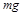, где 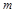– масса груза (в кг), 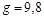м/с2. Во второй столбец перенесите значения длин выбранной пружины 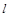(в метрах). Предусмотрите ячейки для средних значени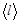й и .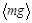


Таблица 10.

 
m, г l, см l, см l, см l, см l, см l, см l, см l, см l, см
11,8 15,4 17,6 19,4 13,2 15,4 19,6 21,4 11,2
12,3 16,5 18,3 21,5 14,3 16,5 21,3 22,4 11,7
13,6 17,6 19,3 21,6 14,8 16,5 22,1 22,6 12,7
14,1 18,2 21,5 22,1 15,6 17,3 21,5 23,7 13,1
16,6 22,3 22,5 24,9 17,6 19,9 23,9 25,5 15,4
21,6 25,6 27,4 29,5 21,4 23,8 27,7 29,9 18,3
22,5 26,4 28,8 31,4 22,6 24,2 28,8 32,1 19,6
23,3 27,9 29,4 31,7 23,8 25,6 29,5 31,7 22,1
26,2 32,1 32,0 34,3 25,5 27,9 31,9 33,6 22,2
27,8 31,4 33,7 35,3 27,6 29,1 33,2 35,3 23,1

 

Таблица 10 (продолжение)

 
m, г l, см l, см l, см l, см l, см l, см l, см l, см l, см
15,1 17,1 19,3 11,4 15,3 19,0 10,8 15,2 19,1
15,6 17,7 19,7 11,6 15,6 19,6 11,5 15,3 19,3
16,7 18,5 21,2 12,0 16,1 20,4 12,3 16,3 20,2
17,3 19,3 21,4 12,5 16,5 20,7 12,4 16,7 20,4
19,4 21,1 23,5 14,9 18,9 22,4 14,2 18,0 21,8
22,3 24,6 26,3 17,4 21,4 25,8 16,5 20,7 24,4
23,5 25,6 27,0 18,2 22,3 26,1 17,2 21,6 25,7
24,4 26,1 28,5 19,4 23,3 27,0 18,4 22,0 26,4
26,4 28,5 31,1 20,3 24,5 28,6 19,3 23,5 27,3
27,0 29,0 31,4 21,9 25,8 29,9 20,7 24,7 28,5

 

3. Возьмите лист миллиметровой бумаги, нанесите на ней оси координат. В соответствии с данными выберите оптимальный масштаб и постройте график зависимости силы тяжести от длины пружины 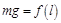, откладывая значения 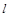вдоль оси Х, а величины 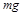вдоль оси Y.

4. Составьте 7 пар точек: 1-4, 2-5, 3-6, 4-7, 5-8, 6-9, 7-10. Методом парных точек рассчитайте 7 коэффициентов наклона 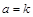по формуле

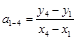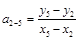, , ... и т.д.

где 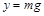, а .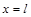

5. Найдите среднее значение 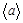, что соответствует среднему значению коэффициента упругости пружины .

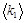6. Найдите среднеквадратичное отклонение 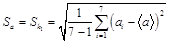, доверительный интервал 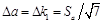, (т.к. получено 7 значений 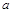). Представьте результат в виде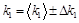

 


Дата добавления: 2016-06-22; просмотров: 1743;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.009 сек.