Гайавата ставит эксперимент .
Если стрелять из лука в сторону мишени, то координаты Х и Y места, куда попадет стрела будут случайными числами. Если выстрелить огромное число раз, то стрелы усеют стену, на которой закреплена мишень, неравномерно. Около центра мишени плотность стрел будет больше, и чем дальше от центра, тем меньше стрел будет приходиться на один квадратный метр. Если посчитать средние значения координат <Х> и <Y>, то, вероятнее всего, они совпадут с координатами центра мишени. Но если во время стрельбы будет дуть сильный ветер все время в одном направлении, то и средние значения координат сместятся в этом направлении. Это можно назвать систематической ошибкой. Чтобы теперь попадать в мишень, надо сделать поправку на ветер. Что же в стрельбе главное – средние значения координат или среднеквадратичное отклонение? Оказывается, можно провести такие стрельбы, где ни одного точного попадания не будет, а средния значения <X> и <Y> указывает ровно в центр мишени. В этом случае важна другая характеристика – кучность, которая непосредственно связана со среднеквадратичным отклонением. Чем меньше 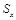 , тем меньше разброс вокруг среднего, тем больше кучность. Таким образом, если мишень мала, то и разброс желательно иметь малым. Но если мишень достаточно большая, то от большого разброса не будет зависеть удачное поражение цели, например, ракета взрывается далеко от летящего самолета противника и поражает цель осколками, разброс которых захватывает большое пространство. Достаточно попадания всего нескольких осколков и цель уничтожена.
, тем меньше разброс вокруг среднего, тем больше кучность. Таким образом, если мишень мала, то и разброс желательно иметь малым. Но если мишень достаточно большая, то от большого разброса не будет зависеть удачное поражение цели, например, ракета взрывается далеко от летящего самолета противника и поражает цель осколками, разброс которых захватывает большое пространство. Достаточно попадания всего нескольких осколков и цель уничтожена.
Морис Дж. Кендалл попытался, затронув поэтические струны души каждого человека, объяснить необходимость привлекать здравый смысл в планировании эксперимента и, особенно, в интерпретации его результатов. Прочитайте песню "Гайавата ставит эксперимент" в Приложении 1.
3.4. Десятичные приставки. Значащие цифры.
Стандартный вид числа
Разные числа содержат разное количество цифр, а некоторые из них могут иметь десятичную запятую. Причём последовательность цифр до запятой (слева от неё) конечна (как минимум одна цифра), а после запятой (справа от неё) — может быть как конечной, так и бесконечной. Например, когда мы делим 1 на 800, то на калькуляторе высвечивается результат 0,00125, представляющий конечную десятичную дробь с пятью цифрами после запятой. Всего в этом числе 6 цифр (три нуля, 1, 2 и 5), но только три из них (1,2 и 5) называются значащими цифрами – это все цифры, начиная с первой слева, отличной от нуля, до последней, за правильность которой можно ручаться (правильность цифр определяется погрешностью измерений).
Часто для компактной записи используют стандартный вид числа:
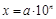 , где
, где 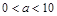 – мантисса (хранитель значащих разрядов в числе),
– мантисса (хранитель значащих разрядов в числе), 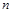 – целое число – называется порядком числа. Например, число х = 0,00125 в стандартном виде будет выглядеть так:
– целое число – называется порядком числа. Например, число х = 0,00125 в стандартном виде будет выглядеть так: 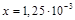 , а стандартный вид числа
, а стандартный вид числа 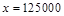 выглядит так:
выглядит так: 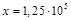 . Чтобы найти порядок числа, надо перенести десятичную запятую на
. Чтобы найти порядок числа, надо перенести десятичную запятую на 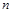 позиций или влево, или вправо до тех пор, пока перед запятой не окажется единственная ненулевая цифра. Если запятая переносится вправо, то к порядку числа добавляется знак минус, если влево – то порядок положителен
позиций или влево, или вправо до тех пор, пока перед запятой не окажется единственная ненулевая цифра. Если запятая переносится вправо, то к порядку числа добавляется знак минус, если влево – то порядок положителен
Если величина в абсолютном исчислении намного больше единицы или, наоборот, намного меньше единицы, то для уменьшения количества нулей часто используют десятичные приставки.
Таблица 5. Десятичные приставки
| Наимено- вание | Обозначе- ние | Множи- тель | Наимено- вание | Обозначе- ние | Множи- тель |
| гига | Г | 109 | санти | с | 10–2 |
| мега | М | 106 | милли | м | 10–3 |
| кило | к | 103 | микро | мк | 10–6 |
| гекто | г | 102 | нано | н | 10–9 |
| деци | д | 10–1 | пико | п | 10–12 |
Например, для сопротивления резистора 120 000 Ом можно применить приставку кило, то есть 120 кОм, или мега – 0,12 МОм. Для силы тока 0,00000123 А подойдет приставка микро, то есть 1,23 мкА = 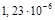 А.
А.
Дата добавления: 2016-06-22; просмотров: 1876;











