Метод линеаризации экспериментальных данных.
Рассмотрим пример другой лабораторной работы по изучению зависимости сопротивления полупроводника 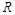 от его температуры
от его температуры 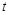 . Диапазон температур полупроводника не очень большой: от комнатной температуры 26°С до 200°С. Предположим, что экспериментальные даненые получены и занесены в таблицу 8.
. Диапазон температур полупроводника не очень большой: от комнатной температуры 26°С до 200°С. Предположим, что экспериментальные даненые получены и занесены в таблицу 8.
Таблица 8. Зависимость температуры полупроводника от температуры.
| t,°C | ||||||||||
| R, Ом |
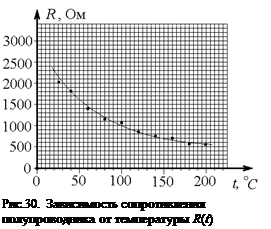 Обсудим еще раз выбор масштаба для представления этих данных в графическом виде (см. рис.30). Максимальная метка
Обсудим еще раз выбор масштаба для представления этих данных в графическом виде (см. рис.30). Максимальная метка 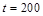 °С, соответствующая оси температур Х, очень неплохо укладывается на 40 клетках, что соответствует очень удобному разделению по 10 клеток на кажые 50°С. А сколько надо дополнительных рисок? В этом случае предлагаю расставить их через 2 клетки, что придаст простоту определения координаты, так как интервал между такими рисками будет соответствовать 10°С, что очень удобно.
°С, соответствующая оси температур Х, очень неплохо укладывается на 40 клетках, что соответствует очень удобному разделению по 10 клеток на кажые 50°С. А сколько надо дополнительных рисок? В этом случае предлагаю расставить их через 2 клетки, что придаст простоту определения координаты, так как интервал между такими рисками будет соответствовать 10°С, что очень удобно.
А вот на оси Y я расставил риски через 5 клеток на кажые 500 Ом сопротивления, что привело к неполному использованию площади бумаги. Но, посудите сами, если разделить ось по 6 или 7 клеток, было бы неудобно находить координату, а если по 8 клеток, то максимальная риска, соответствующая 2000 Ом, не поместилась бы на оси.
Теперь надо обсудить вид теоретической кривой. Откроем методические указания по выполнению лабораторных работ [2] на странице 28 и найдем фомулу 3, описывающую зависимость сопротивления полупроводника от темепературы 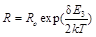 ,
,
где 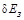 – ширина запрещенной зоны,
– ширина запрещенной зоны, 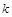 – постоянная Больцмана,
– постоянная Больцмана, 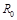 – некоторая константа, имеющая размерность сопротивления, и, наконец, температура
– некоторая константа, имеющая размерность сопротивления, и, наконец, температура 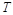 , выраженная в Кельвинах. Начнем оформлять новую таблицу. Во-первых, температуру переведем в Кельвины. Во-вторых, поставим себе задачу не только нарисовать новый график
, выраженная в Кельвинах. Начнем оформлять новую таблицу. Во-первых, температуру переведем в Кельвины. Во-вторых, поставим себе задачу не только нарисовать новый график 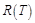 , но и найти с помощью графика ширину запрещенной зоны. Для этого прологарифмируем экспоненциальную зависимость и получим
, но и найти с помощью графика ширину запрещенной зоны. Для этого прологарифмируем экспоненциальную зависимость и получим 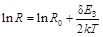
Обозначим 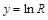 ,
, 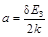 ,
, 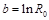 и
и 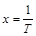 . Тогда получим линейную зависимость
. Тогда получим линейную зависимость 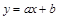 ,
,
которую мы и будем изображать на графике. Данные, соответствующие значениям 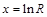 и
и 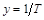 , запишем в таблицу 9.
, запишем в таблицу 9.
Таблица 9. Пересчет данных таблицы 8.
| номер точки | ||||||||||
| T, K | ||||||||||
| 1/T, 10–3 K–1 | 3,34 | 3,19 | 3,00 | 2,83 | 2,68 | 2,54 | 2,42 | 2,31 | 2,21 | 2,11 |
| lnR, Ом | 7,62 | 7,51 | 7,25 | 7,06 | 6,99 | 6,74 | 6,61 | 6,56 | 6,36 | 6,34 |
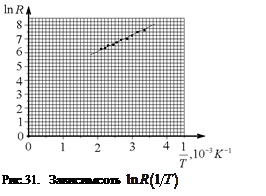 Если по данным таблицы 9 построить график зависимости
Если по данным таблицы 9 построить график зависимости 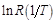 на рис.31, то все экспериментальные точки займут совсем немного места на листе при большом пустом пространстве. Почему так получилось? Потому что по осям Х и Y метки расставлены начиная от 0, хотя значения, например,
на рис.31, то все экспериментальные точки займут совсем немного места на листе при большом пустом пространстве. Почему так получилось? Потому что по осям Х и Y метки расставлены начиная от 0, хотя значения, например, 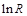 начинаются только со значения
начинаются только со значения 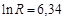 . Обязательно ли делать начальную метку равную 0? Ответ на этот вопрос зависит от поставленных задач. В примере с маятником Обербека (см. рис.28) было очень важным найти пересечение оси Х теоретической прямой в точке с координатой Y=0, что соответствовало значению
. Обязательно ли делать начальную метку равную 0? Ответ на этот вопрос зависит от поставленных задач. В примере с маятником Обербека (см. рис.28) было очень важным найти пересечение оси Х теоретической прямой в точке с координатой Y=0, что соответствовало значению  . А в этой задаче надо найти только ширину запрещенной зоны, которая связана с постоянной
. А в этой задаче надо найти только ширину запрещенной зоны, которая связана с постоянной 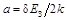 , соответствующая коэффициенту наклона прямой на рис.31, поэтому совсем не обязательно расставлять метки на осях, начиная с 0.
, соответствующая коэффициенту наклона прямой на рис.31, поэтому совсем не обязательно расставлять метки на осях, начиная с 0.
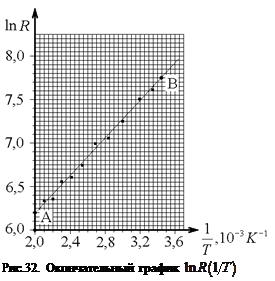 Изучая данные из табл.9 и подбирая удобный масштаб, можно с уверенностью сказать, что ориентацию миллиметровой бумаги нужно изменить, как показано на рис.32. Самостоятельно изучите выбранный масштаб и убедитесь в том, что он очень удобен для работы с графиком. На теоретической прямой (проведенной на глаз наилучшим способом между экспериментальными точками) поставим две точки А и В с координатами
Изучая данные из табл.9 и подбирая удобный масштаб, можно с уверенностью сказать, что ориентацию миллиметровой бумаги нужно изменить, как показано на рис.32. Самостоятельно изучите выбранный масштаб и убедитесь в том, что он очень удобен для работы с графиком. На теоретической прямой (проведенной на глаз наилучшим способом между экспериментальными точками) поставим две точки А и В с координатами 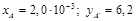 и
и 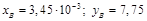 . Коэффициент наклона
. Коэффициент наклона 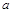 выразим через координаты этих точек по формуле
выразим через координаты этих точек по формуле
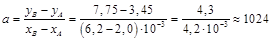 .
.
И, наконец, вычисляем ширину запрещенной зоны
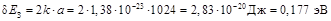 .
.
Методом парных точек рассчитаем этот же коэффициент 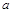 и его погрешность
и его погрешность 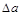 , для этого рассмотрим пары точек из таблицы 9:
, для этого рассмотрим пары точек из таблицы 9:
1–4, 2–5, 3–6, 4–7, 5–8, 6–9 и 7–10.
Рассчитаем для этих пар точек коэффициенты наклона прямых, которые проходят через них
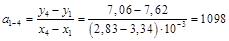
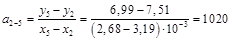
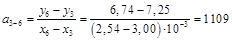
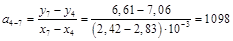
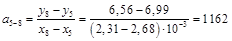
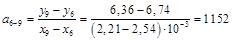
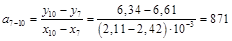
Среднее значение 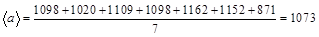
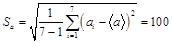 ,
, 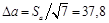
Теперь рассчитаем ширину запрещенной зоны 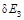 и ее погрешность
и ее погрешность 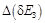 .
.
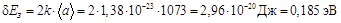
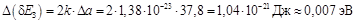
Таким образом мы пришли к ответу
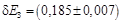 эВ
эВ
Дата добавления: 2016-06-22; просмотров: 2655;











