Новый закон формирования электрической мощности
Большая часть электрической энергии с момента начала её применения и по настоящее время генерируется в виде непрерывного напряжения. Эта непрерывность была заложена вначале в алгоритмы, а потом и электронные программы электроизмерительных приборов, учитывающих расход электроэнергии. Когда началось импульсное использование электрической энергии, то для её учета математики разработали графоаналитический метод, в котором допустили глобальную физико-математическую ошибку. Она завышает расход электроэнергии, потребляемой импульсами в количество раз, равное скважности импульсов напряжения.
Скважностью импульсов 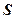 называется величина, равная отношение ллительности периода
называется величина, равная отношение ллительности периода 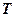 следования импульсов к длительности импульсов
следования импульсов к длительности импульсов 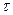 , то есть
, то есть 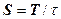 .
.
Покажем суть физико-математической ошибки учёта электроэнергии, потребляемой импульсами и докажем её достоверность теоретически и экспериментально. Величина, генерируемой и реализуемой электрической мощности, рассчитывается по хорошо известной формуле
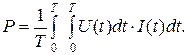 . (327)
. (327)
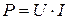 . (328)
. (328)
и результат расчёта по этой формуле совпадает с показаниями всех приборов (рис. 167, а). Никаких противоречий в показаниях приборов в этом случае нет. Они появляются, если электроэнергия потребляется импульсами (рис. 167, b).
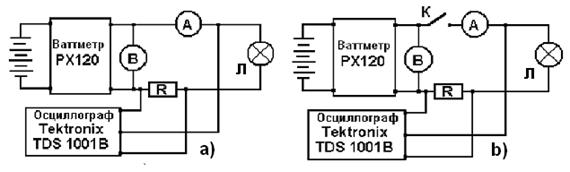
Рис. 167. Схема для измерения напряжения, тока и мощности,
реализуемой аккумулятором: а) на непрерывное питание лампочки Л;
b) на импульсное питание лампочки Л
Для проверки этого факта введём в схему (рис. 167, а) электронный ключ К (рис. 167, b), который будет подавать на клеммы лампочки импульсы напряжения с амплитудами 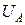 , а они, вместе с нагрузкой (лампочка), будут формировать импульсы тока с амплитудами
, а они, вместе с нагрузкой (лампочка), будут формировать импульсы тока с амплитудами 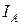 .
.
Считается, что все счётчики электроэнергии универсальны и точно измеряют количество электрической энергии, переданное потребителю по любому закону: синусоидальному, хаотическому или импульсному.
Алгоритм, заложенный в счётчик электроэнергии, следует из математической модели (327). Если электроэнергия подаётся
потребителю непрерывно, то работает первая, интегральная часть формулы (327). Когда электроэнергия подаётся потребителю импульсами со скважностью 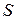 , равной отношению длительности периода
, равной отношению длительности периода 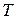 подачи импульсов к длительности импульса
подачи импульсов к длительности импульса 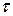 (
( 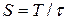 ), то графоаналитический метод решения уравнения (327) приводит его к простому виду, представленному в конце формулы (329).
), то графоаналитический метод решения уравнения (327) приводит его к простому виду, представленному в конце формулы (329).

|
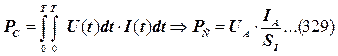
|
Более 100 лет все специалисты считали, что конечная часть формулы (329) правильно учитывает среднюю величину электрической мощности, реализуемой импульсно. Проверим это путём анализа осциллограммы импульсов напряжения и тока на клеммах аккумулятора, энергия которого расходуется импульсами (рис. 168).
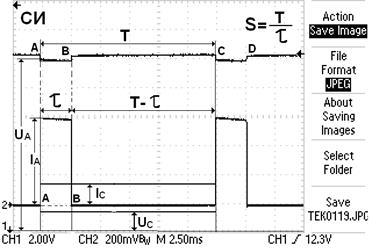
| Старый закон
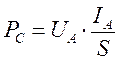 (329)
Новый закон (329)
Новый закон
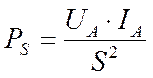 (330) (330)
|
Рис. 168. Осциллограмма импульсов напряжения 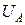 и тока
и тока 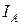 ,
,
снятая с клемм аккумулятора
Чтобы понять физический процесс формирования средней величины электрической импульсной мощности, реализуемой аккумулятором, проанализируем тщательно осциллограмму, снятую с клемм аккумулятора (рис. 168).
Если энергия потребляется импульсами из аккумулятора, то, как считается, её средняя мощность 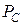 определяется по конечному выражению формулы (329), которая представлена и на рис. 168.
определяется по конечному выражению формулы (329), которая представлена и на рис. 168.
Как мы уже отметили, для описания импульсного расхода или импульсного потребления электроэнергии с длительностью импульсов 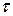 и периодичностью их следования
и периодичностью их следования 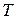 вводится понятие скважность
вводится понятие скважность 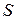 импульсов, равная отношению длительности периода
импульсов, равная отношению длительности периода 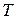 формирования импульсов к длительности импульсов
формирования импульсов к длительности импульсов 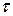 , то есть
, то есть 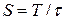 (рис. 168).
(рис. 168).
Нагрузка включается в момент обозначенный буквой А (рис. 168). Хорошо видно, как в этот момент номинальное напряжение на клеммах аккумулятора уменьшается до амплитудной величины 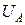 (рис. 168). Одновременно появляется ток с амплитудой
(рис. 168). Одновременно появляется ток с амплитудой 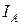 . Длительности импульса
. Длительности импульса 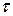 тока и напряжения одинаковые. В точке В подача напряжения потребителю отключается и амплитуды напряжения и тока принимают нулевые значения (рис. 168).
тока и напряжения одинаковые. В точке В подача напряжения потребителю отключается и амплитуды напряжения и тока принимают нулевые значения (рис. 168).
Более 100 лет никто не обращал внимания на то, что после выключения подачи напряжения потребителю, в точке В напряжение на клеммах аккумулятора восстанавливается до номинальной величины. Это значит, что прекращается расход электроэнергии из аккумулятора. Длительность отсутствия расхода электроэнергии аккумулятором равна разности между длительностью периода 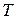 подачи импульсов потребителю и длительностью импульса
подачи импульсов потребителю и длительностью импульса 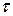 , то есть
, то есть 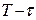 (рис. 168).
(рис. 168).
В точке С подача напряжения потребителю вновь включается и номинальное напряжение на клеммах аккумулятора вновь уменьшается до рабочей амплитудной величины 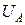 . Сразу же появляется и ток с прежней амплитудой
. Сразу же появляется и ток с прежней амплитудой 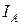 .
.
Итак, при импульсном расходе электроэнергии периодичность изменения длительности 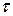 амплитуд напряжения
амплитуд напряжения 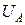 и тока
и тока 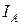 одинаковая. Но старый закон формирования средней величины импульсной мощности (329) отрицает очевидность периодичности изменения амплитуды напряжения
одинаковая. Но старый закон формирования средней величины импульсной мощности (329) отрицает очевидность периодичности изменения амплитуды напряжения 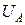 . Это отрицание скрыто в ошибочности формулы (329). Суть ошибочности в том, что амплитуда напряжения
. Это отрицание скрыто в ошибочности формулы (329). Суть ошибочности в том, что амплитуда напряжения 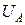 в конечном выражении формулы (329) не изменяет своей величины в интервале периода
в конечном выражении формулы (329) не изменяет своей величины в интервале периода 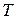 а осциллограмма (рис. 168) убеждает нас в обратном. Из неё следует, что амплитудная величина напряжения
а осциллограмма (рис. 168) убеждает нас в обратном. Из неё следует, что амплитудная величина напряжения 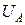 работает только в интервале длительности импульса
работает только в интервале длительности импульса 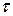 (на рис. 168 интервал А-В). В интервале ВС, то есть
(на рис. 168 интервал А-В). В интервале ВС, то есть 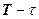 напряжение отключено, а академическая формула (329) убеждает нас, что оно продолжает работать всей своей амплитудной величиной
напряжение отключено, а академическая формула (329) убеждает нас, что оно продолжает работать всей своей амплитудной величиной 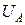 в интервале всего периода
в интервале всего периода 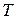 , то есть в интервале АС (рис. 168).
, то есть в интервале АС (рис. 168).
Более 100 лет нас пытаются убедить, что при импульсном потреблении электроэнергии изменяется лишь средняя величина тока. Математически это изменение записывается так 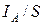 . Это - средняя величина тока
. Это - средняя величина тока 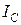 . Запись
. Запись 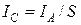 означает, что импульс тока растянут так, что его средняя величина
означает, что импульс тока растянут так, что его средняя величина 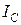 действует, как бы непрерывно, в течение всего периода
действует, как бы непрерывно, в течение всего периода 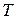 , превращаясь из вертикально расположенного прямоугольника с длительностью
, превращаясь из вертикально расположенного прямоугольника с длительностью 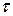 в горизонтальный прямоугольник с длительностью периода
в горизонтальный прямоугольник с длительностью периода 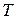 и амплитудой
и амплитудой 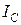 (рис. 168). Эта процедура соответствует системе СИ, которая требует непрерывного участия тока в формировании средней величины импульсной мощности
(рис. 168). Эта процедура соответствует системе СИ, которая требует непрерывного участия тока в формировании средней величины импульсной мощности 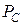 (327) и (328).
(327) и (328).
Нетрудно видеть, что старый закон (329) формирования средней величины импульсной мощности ловко обманывает нас. В нём напряжение действует непрерывно всей своей амплитудной величиной 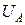 в интервале всего периода
в интервале всего периода 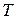 и создаётся впечатление, что это соответствует системе СИ и поэтому правильно.
и создаётся впечатление, что это соответствует системе СИ и поэтому правильно.
Этому ложному академическому представлению верят более 100 лет. В чём сущность этого ложного представления? Смотрим внимательно на осциллограмму ещё раз и видим, что амплитудная величина напряжения 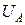 действует только в интервале длительности импульса
действует только в интервале длительности импульса 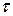 и напряжения и тока, то есть в интервале от точки А до точки В (рис. 168). После точки В подача напряжения от аккумулятора прекращается. Свидетельством этого является увеличение в точке В напряжения на клеммах аккумулятора до номинальной величины. В результате в интервале от точки В до точки С, равному временному интервалу
и напряжения и тока, то есть в интервале от точки А до точки В (рис. 168). После точки В подача напряжения от аккумулятора прекращается. Свидетельством этого является увеличение в точке В напряжения на клеммах аккумулятора до номинальной величины. В результате в интервале от точки В до точки С, равному временному интервалу 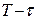 , аккумулятор не расходует свою энергию. Старая математическая модель (329) закона сохранения энергии убеждает нас в обратном. Из неё следует, что амплитудная величина напряжения
, аккумулятор не расходует свою энергию. Старая математическая модель (329) закона сохранения энергии убеждает нас в обратном. Из неё следует, что амплитудная величина напряжения 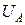 действует не в интервале длительности импульса
действует не в интервале длительности импульса 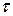 , а в интервале всего периода
, а в интервале всего периода 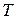 . Эта явная ошибка оставалась незамеченной более 100 лет. Теперь мы ясно видим, что для выполнения требований системы СИ, мы обязаны поступить с амплитудой напряжения так же, как и с амплитудой тока, то есть амплитуду напряжения
. Эта явная ошибка оставалась незамеченной более 100 лет. Теперь мы ясно видим, что для выполнения требований системы СИ, мы обязаны поступить с амплитудой напряжения так же, как и с амплитудой тока, то есть амплитуду напряжения 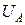 надо разделить на скважность импульсов
надо разделить на скважность импульсов 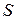 . Это будет означать, что вертикальный прямоугольный импульс напряжения с амплитудой
. Это будет означать, что вертикальный прямоугольный импульс напряжения с амплитудой 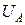 и с длительностью
и с длительностью 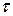 (рис. 168) превратится в горизонтальный – с амплитудой
(рис. 168) превратится в горизонтальный – с амплитудой 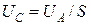 и длительностью, равной длительности всего периода
и длительностью, равной длительности всего периода 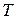 , что соответствует требованию системы СИ.
, что соответствует требованию системы СИ.
Итак, описанное убедительно доказывает, что средняя величина импульсной мощности равна произведению средних значений амплитуд напряжения
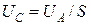 (331)
(331)
и тока
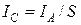 , (332)
, (332)
то есть
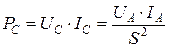 . (333→330)
. (333→330)
В результате появляется математическая модель (330) нового закона формирования средней величины электрической мощности, которая отражает реальность.
Удивительно то, что простота описанной логики анализа осциллограммы, снятой с клемм аккумулятора, питающего потребитель импульсами напряжения и тока, доступна для понимания школьникам, а академики всех академий мира не понимают её более 100 лет. Представим результаты экспериментов, доказывающих ошибочность академических представлений о формировании средней величины импульсной электрической мощности.
Для этого используем импульсный электромотор-генератор, изобретённый в России. Он может работать в режиме электромотора и в режиме электромотора-генератора, производя дополнительную электроэнергию (рис. 169).
Электромотор-генератор МГ-2 (рис. 169) проработал в режиме поочерёдной разрядки одного аккумулятора и зарядки другого и питал электролизёр 3 часа 10 минут. За это время напряжение на клеммах аккумуляторов упало на 0,3В. Это значит, что при питании электромотора-генератора МГ-2, который получал энергию от аккумулятора, часть её передавал электролизёру, а часть - на зарядку другого аккумулятора. В результате напряжение на клеммах каждого из двух аккумуляторов упало за 3 часа 10 минут на 0,3В (табл. 43).


Рис. 169. Импульсный электромотор-генератор МГ-2, аккумуляторы 6МТС-9 для мотоцикла и ячейка электролизёра
Таблица 43. Разрядка аккумуляторов, питавших МГ-2, который питал электролизёр и часть энергии возвращал аккумуляторам в течение 3 часов 10 мин
| Номера аккумуляторов | Начальное напряжение, В | Конечное напряжение, В |
| 1 (разрядка) | 12,28 | 12,00 |
| 2 (разрядка) | 12,33 | 12,00 |
Приборы зафиксировали среднюю величину напряжения 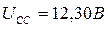 и среднюю величину тока
и среднюю величину тока 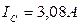 . Расчёт величины средней импульсной мощности, реализуемой аккумуляторами по формуле (329), даёт такой результат
. Расчёт величины средней импульсной мощности, реализуемой аккумуляторами по формуле (329), даёт такой результат
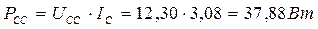 . (334)
. (334)
Количество электроэнергии, израсходованной аккумуляторами, равно
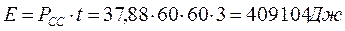 (335)
(335)
При непрерывной реализации мощности, следующей из показаний приборов, падение напряжения на клеммах каждого аккумулятора должно было составить
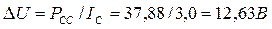 . (336)
. (336)
Это явно противоречит реальности. Приборы зафиксировали падение напряжения на клеммах каждого аккумулятора на 0,3В (табл. 43). Если учитывать реальное падение напряжения на клеммах аккумуляторов за время их работы, то каждый аккумулятор потерял энергию, равную
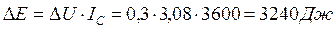 . (337)
. (337)
Итак, явное противоречие, которое побуждает нас рассчитать реальную мощность, которую реализовывали аккумуляторы, работая более 3 часов. Вот она.
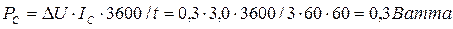 . (338)
. (338)
Это почти в 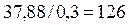 раз меньше показаний приборов (334).
раз меньше показаний приборов (334).
Из процесса взаимодействия магнитных полюсов постоянных магнитов (рис. 170) следует, что если у двух параллельных проводов ток будет течь в одном направлении (рис. 170, с), то силовые линии магнитных полей, формирующихся в плоскости, перпендикулярной проводам, в зоне их контакта будут направлены навстречу друг другу и провода будут сближаться (рис. 170, с), как разноименные полюса магнитов (рис. 126, а).
Если же направление тока у параллельных проводов будет противоположно (рис. 170, d), то направления магнитных силовых линий образующихся при этом магнитных полей будут совпадать по направлению в зоне их контакта, и такие провода будут удаляться друг от друга (рис. 170, d), как и одноименные полюса стержневых магнитов.
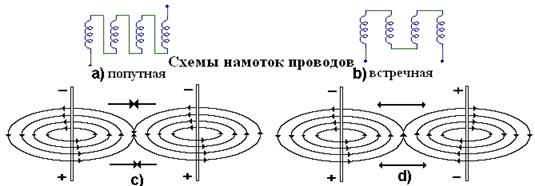
Рис. 170. Схемы намоток проводов и взаимодействия их магнитных полей
А теперь обратим внимание на существующие схемы намотки проводов на магнитопроводы роторов и статоров электромоторов (рис. 170, а и b). Вначале наматывается первый слой витков проводов в выбранном направлении. Как только первый слой витков уложен, то с конца, где он уложен (рис. 170, b), начинается укладка второго слоя и т. д.
В результате магнитные поля, которые формируются между витками, стремятся удалить их друг от друга (рис. 170, d). Вполне естественно, что этот процесс ослабляет суммарное магнитное поле в зоне контакта витков провода (рис. 170, b).
Если же провода укладывать так, чтобы после завершения первого слоя витков, второй начинать с того конца магнитопровода, с которого начинался первый слой (рис. 170, а). То, при такой схеме намотки ток в витках обоих слоёв проводов будет течь в одном направлении (рис. 170, с) и магнитные поля витков будут сближать их, усиливая суммарное магнитное поле (рис. 170, с). В результате ротор, с попутной намоткой проводов (рис. 170, а) должен вращаться быстрее, ротора со встречной намоткой (рис. 170, b).
Достоверность этого следствия новой электрофотонодинамики была доказана с помощью электромотора – генератора МГ-2, ротор которого представлен на рис. 171. Результаты эксперимента представлены в табл. 44.
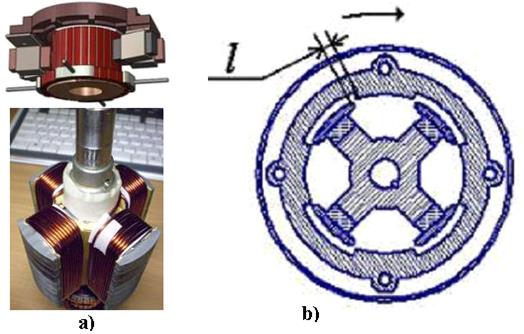
Рис. 171: а) ротор МГ-2; b) схема разреза ротора и статора МГ-2
Таблица 44. Влияние схем намотки проводов на роторе электромотора-генератора на его обороты.
| Встречная намотка (рис. 170, b) | Попутная намотка (рис. 170, а) | ||
| количество витков - 40 | количество витков – 38 | ||
| напряжение/ток, В/А | обороты в минуту | напряжение/ток, В/А | обороты в минуту |
| 12/1,6 | 12/1,7 | ||
| 24/1,6 | 24/1,7 | ||
| 36/1,6 | 36/1,7 |
Как видно (табл. 44), новая попутная намотка проводов на роторе (рис. 171, а) увеличивает его обороты при той же входной мощности.
Влияние момента подачи напряжения в обмотку возбуждения ротора, при сближении магнитных полюсов ротора и статора (рис. 171, b) на обороты ротора на холостом ходу при разных вариантах намотки ротора представлено в табл. 44 и 45.
Таблица 45. Влияние момента начала подачи напряжения в обмотку возбуждения ротора на обороты ротора на холостом ходу
при встречной намотке проводов на роторе (рис. 170, b)
Опережение
подачи
напряжения, 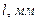
| Среднее напряжение, В | Средний ток, А | Средняя мощность, Вт | Обороты
ротора,
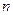 об./мин об./мин
|
| 0,00 | 3,83 | 1,25 | 4,80 | |
| 5,00 | 3,14 | 1,05 | 3,30 | |
| 10,00 | 3,28 | 1,17 | 3,84 | |
| 15,00 | 4,41 | 1,32 | 5,82 | |
| 20,00 | 7,30 | 1,52 | 11,10 | |
| 25,00 | 7,90 | 1,52 | 12,00 | |
| 30,00 | 10,00 | 1,40 | 14,00 |
Таблица 46. Влияние момента начала подачи напряжения в обмотку возбуждения ротора на обороты ротора на холостом ходу при
попутной намотке проводов (рис. 170, a)
Опережение
подачи
напряжения, 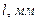
| Среднее напряжение, В | Средний ток, А | Средняя мощность, Вт | Обороты ротора,
 об./мин об./мин
|
| 0,00 | 7,80 | 1,56 | 12,00 | |
| 10,00 | 7,64 | 1,56 | 11,92 | |
| 20,00 | 7,35 | 2,16 | 15,87 | |
| 27,00 | 7,70 | 2,20 | 16,94 |
Заключение
Изготовленные и испытанные первые в мире российские электромоторы – генераторы МГ-1, МГ-2 и МГ-3, вырабатывающие и потребляющие электроэнергию импульсами, убедительно доказали достоверность нового закона формирования импульсной электрической мощности (330) и полную ошибочность старого (329).
Дата добавления: 2016-06-22; просмотров: 2993;











