Расчет спектра атома бериллия
Атом бериллия имеет четыре электрона. Наибольшую энергию ионизации имеет четвертый электрон, а наименьшую – первый. Не будем приводить расчет спектра четвертого электрона этого атома, так как его результаты приведены в табл. 10, как спектра водородоподобного атома. Не будем полностью повторять детали методики расчета спектров третьего, второго и первого электронов этого атома, а приведем лишь ключевые моменты этой методики.
Энергия ионизации третьего электрона атома бериллия равна 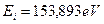 . Энергии возбуждения этого электрона, соответствующие стационарным энергетическим уровням, составляют следующий ряд [А. П. Стриганов]: 123,67; 140,39; 146,28; 149,01; 150,50; 151,40 eV. Разность между энергией ионизации и значением первой энергии в этом ряду будет равна
. Энергии возбуждения этого электрона, соответствующие стационарным энергетическим уровням, составляют следующий ряд [А. П. Стриганов]: 123,67; 140,39; 146,28; 149,01; 150,50; 151,40 eV. Разность между энергией ионизации и значением первой энергии в этом ряду будет равна
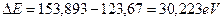 . (190)
. (190)
Энергия связи третьего электрона с ядром атома, соответствующая первому энергетическому уровню, определится так
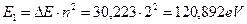 . (191)
. (191)
Подставляя значения 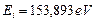 и
и 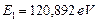 в формулы (178) и (180), найдем (табл. 18).
в формулы (178) и (180), найдем (табл. 18).
Таблица 18. Спектр третьего электрона атома бериллия
| Значения | n | |||||
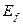 (эксп.) (эксп.)
| eV | 123,7 | 140,4 | 146,3 | 149,0 | 150,5 |
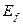 (теор.) (теор.)
| eV | 123,7 | 140,5 | 146,3 | 149,0 | 150,5 |
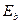 (теор.) (теор.)
| eV | 30,22 | 13,43 | 7,56 | 4,84 | 3,36 |
Второй электрон атома бериллия имеет энергию ионизации 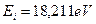 и следующий ряд энергий возбуждения, соответствующих стационарным энергетическим уровням [А.П. Строганов]: 3,96; 11,96; 14,7; 15,99; 16,67; 17,08 eV.
и следующий ряд энергий возбуждения, соответствующих стационарным энергетическим уровням [А.П. Строганов]: 3,96; 11,96; 14,7; 15,99; 16,67; 17,08 eV.
Обратим внимание на то, что величина энергии 3,96eV явно выходит за пределы предполагаемой нами закономерности формирования энергий возбуждения. В справочнике [А.Н. Зайдель] эта спектральная линия значится яркой, поэтому у нас нет оснований исключать её из рассмотрения. У нас остается одна возможность - предположить, что второй электрон атома бериллия может иметь два положения в атоме и связано это со структурой его ядра. Дальше мы будем анализировать структуры ядер атомов и попытаемся найти ответ на возникшую неясность. Сейчас же у нас остаётся одна возможность: считать, что энергия возбуждения 3,96eV и оставшиеся энергии 11,96; 14,7; 15,99; 16,67; 17,08 eV соответствуют разным положениям второго электрона в атоме, поэтому мы попытаемся получить теоретически только ряд 11,96; 14,7; 15,99; 16,67; 17,08 eV. Для этого найдем разность между энергией ионизации 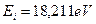 и энергией 11,96eV.
и энергией 11,96eV.
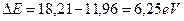 . (192)
. (192)
Тогда энергия связи второго электрона атома бериллия, соответствующая первому фиктивному энергетическому уровню, окажется такой: 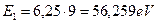 . Подставляя эту величину и энергию ионизации
. Подставляя эту величину и энергию ионизации 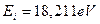 в формулы (178) и (180), найдем (табл. 19).
в формулы (178) и (180), найдем (табл. 19).
Таблица 19. Спектр второго электрона атома бериллия
| Значения | n | |||||
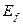 (эксп.) (эксп.)
| eV | - | 11,96 | 14,72 | 15,99 | 16,67 |
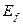 (теор.) (теор.)
| eV | 4,15 | 11,96 | 14,70 | 15,96 | 16,65 |
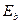 (теор.) (теор.)
| eV | 14,81 | 6,25 | 3,52 | 2,25 | 1,56 |
Теория предсказывает (табл. 19) существование энергии возбуждения 4,15eV, соответствующей второму энергетическому уровню, но это, по – видимому, фиктивная величина энергии. Причину этой фиктивности мы выясним при алализе структуры атома бериллия.
Первый электрон атома бериллия имеет энергию ионизации 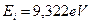 и следующий ряд энергий возбуждения [А.П. Стриганов]: 2,73; 5,28; 7,46; 8,31; 8,69 eV. Отметим, что в справочнике [А.Н. Зайдель] нет энергии 2,73 eV, а в справочнике [А.П. Стриганов] она приведена без указания её яркости. Это даёт нам основание исключить её из рассмотрения. Тогда разность энергий будет равна
и следующий ряд энергий возбуждения [А.П. Стриганов]: 2,73; 5,28; 7,46; 8,31; 8,69 eV. Отметим, что в справочнике [А.Н. Зайдель] нет энергии 2,73 eV, а в справочнике [А.П. Стриганов] она приведена без указания её яркости. Это даёт нам основание исключить её из рассмотрения. Тогда разность энергий будет равна 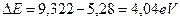 , а энергия, соответствующая первому фиктивному энергетическому уровню, окажется такой
, а энергия, соответствующая первому фиктивному энергетическому уровню, окажется такой 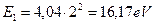 . Подставляя
. Подставляя 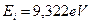 и
и 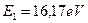 в формулы (178) и (180), найдем (табл. 20).
в формулы (178) и (180), найдем (табл. 20).
Пока что математические модели (178) и (180) дали удовлетворительные результаты. Однако это были спектры атомов и ионов первых четырех элементов таблицы Д.И. Менделеева. Это самые простые атомы.
Таблица 20. Спектр первого электрона атома бериллия
| Значения | n | |||||||
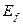 (эксп.) (эксп.)
| eV | 5,28 | 7,46 | 8,31 | 8,69 | 8,86 | 8,98 | 9,07 |
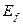 (теор.) (теор.)
| eV | 5,28 | 7,53 | 8,31 | 8,67 | 8,87 | 8,99 | 9,07 |
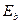 (теор.) (теор.)
| eV | 4,04 | 1,80 | 1,01 | 0,65 | 0,45 | 0,33 | 0,25 |
Примечание: экспериментальные значения энергий возбуждения, соответствующие 6-му, 7-му и 8-му энергетическим уровням взяты из справочника [А.Н. Зайдель].
Если электроны действительно прецессируют на ядрах атомов, то при увеличении их количества в атоме они начинают взаимодействовать друг с другом, что не учитывают математические модели (178) и (180). Поскольку процесс прецессирования электрона сопровождается изменением положения его спина 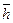 , то этот процесс должен сопровождаться поглощением или излучением фотонов. В результате спектральная линия будет расширяться или вместо спектральной линии будут образовываться светлые полосы, что и наблюдается в молекулярных спектрах. Есть основания полагать, что для атомов с большим количеством электронов и для молекул в математических моделях (178), (180) появятся поправочные коэффициенты или тригонометрические функции, которые будут характеризовать прецессию электрона в ячейке атома. Под ячейкой мы понимаем полость конической формы, в основании которой расположен электрон, а вершина направлена к ядру атома.
, то этот процесс должен сопровождаться поглощением или излучением фотонов. В результате спектральная линия будет расширяться или вместо спектральной линии будут образовываться светлые полосы, что и наблюдается в молекулярных спектрах. Есть основания полагать, что для атомов с большим количеством электронов и для молекул в математических моделях (178), (180) появятся поправочные коэффициенты или тригонометрические функции, которые будут характеризовать прецессию электрона в ячейке атома. Под ячейкой мы понимаем полость конической формы, в основании которой расположен электрон, а вершина направлена к ядру атома.
Возникает вопрос: какую цель можно преследовать, рассчитывая спектры атомов и ионов. Первая цель - получение информации для выявления структуры атома и его ядра. Вторая цель - расчет энергий связей валентных электронов с ядрами атомов для использования их при анализе энергетического баланса в различных химических реакциях. Первая цель представляется далекой и, тем не менее, мы сделаем первые шаги к этой цели. Вторая цель ближе к практике и поэтому заслуживает приоритетного внимания. С учетом этого дальше мы будем пытаться рассчитывать спектры валентных электронов.
При анализе структуры ядер атомов и самих атомов химических элементов мы увидим, что если в атоме находятся все электроны, то их энергии связи с протонами ядер, примерно, одинаковые.
Мы уже условились называть электрон с наименьшим потенциалом ионизации первым электроном. Именно этот электрон является валентным. Дальше мы увидим, что ядра атомов имеют такую структуру, при которой сразу несколько электронов имеют равные потенциальные возможности быть валентными электронами. Поэтому нумерация электронов в атоме – дело условное. Попытаемся рассчитать спектр электрона атома бора, имеющий наименьший потенциал ионизации. Назовем этот электрон первым.
Дата добавления: 2016-06-22; просмотров: 2896;











