Рисование плоских фигур

Для того чтобы перейти к рисованию геометрических тел, необходимо рассмотреть построение геометрических фигур на плоскости.

Построим правильный треугольник. Треугольник называется правильным, если все его стороны равны, а углы при вершинах составляют 60°. Для построения правильного треугольника необходимо провести горизонтальную и вертикальную прямые (рисунок 4), точку пересечения прямых обозначим О.

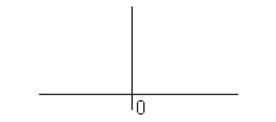
Рисунок 4 – Первый этап построения правильного треугольника

Затем выбираем длину единичного отрезка и откладываем на горизонтальной прямой от точки О три отрезка вправо и влево. На вертикальной прямой нужно отложить пять единичных отрезков (рисунок 5).

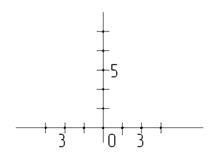
Рисунок 5 – Второй этап построения правильного треугольника

Соединим построенные точки, получим правильный треугольник (рисунок 6).

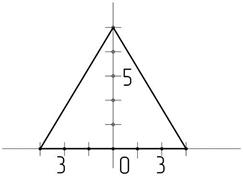
Рисунок 6 – Заключительный этап построения правильного

треугольника

Построим правильный шестиугольник. Для этого сначала проведем горизонтальную и вертикальную прямые, точку пересечения линий обозначим О. Затем на данных прямых отложим от точки О единичные отрезки, на которых построим квадрат (рисунок 7).

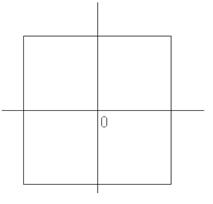
Рисунок 7 – Первый этап построения правильного шестиугольника

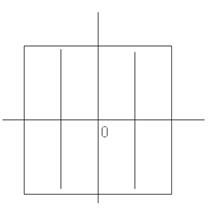
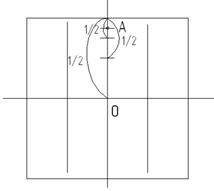
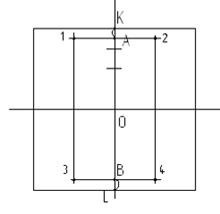
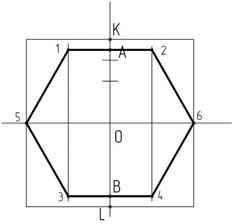
Теперь горизонтальные отрезки поделим пополам и проведем через полученные точки вертикальные прямые, как показано на рисунке 8 а. Отрезки, находящиеся на вертикальной прямой, поделим последовательно три раза пополам, причем каждый раз пополам нужно делить верхнюю часть нового отрезка (рисунок 8 б). Последнюю точку обозначим А. Проведем через нее горизонтальную прямую до пересечения с вертикальными линиями, точки пересечения обозначим 1 и 2. Получили две вершины правильного шестиугольника. Симметрично относительно горизонтальной прямой будут находиться еще две вершины шестиугольника. Чтобы найти их положение, нужно зрительно измерить длину отрезка АК и отложить ее от точки L на вертикальной прямой. Получим точку В (рисунок 9 а). Проведем через точку В горизонтальную прямую до пересечения с вертикальными линиями построим точки 3 и 4 (рисунок 9 б). Пятая и шестая вершины шестиугольника находятся в точках пересечения сторон квадрата с горизонтальной прямой. Соединим построенные точки, получим изображение правильного шестиугольника.

а	б

а – второй этап построения шестиугольника; б – построение точки А

Рисунок 8 – Этапы построения шестиугольника

а	б

а – построение вершин шестиугольника; б – результат построений

Рисунок 9 – Этапы построения шестиугольника

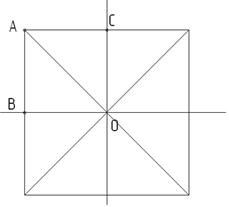
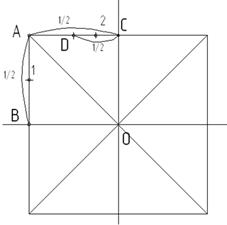
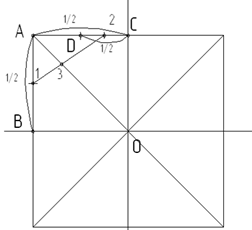
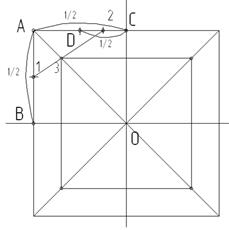
Рассмотрим построение окружности. Окружность можно построить способом вписывания ее в квадрат при помощи восьми точек. Построение начинаем с проведения горизонтальной и вертикальных прямых, точку их пересечения обозначим О. Затем на данных прямых отложим от точки О единичные отрезки, на которых построим квадрат (рисунок 7). Проведем в квадрате диагонали. Обозначим характерные точки (они нужны для построения окружности). Так, левая верхняя точка квадрата – точка А, а точки пересечения горизонтальной и вертикальной прямых со сторонами квадрата – точки В и С, соответственно (рисунок 10 а). Затем отрезок АВ разделим пополам, получим точку 1, а отрезок АС – сначала пополам, отметим точку D, а затем отрезок DC тоже разделим пополам, отметим точку 2 (рисунок 10 б). Соединим точки 1 и 2, найдем пересечение отрезка 12 с диагональю квадрата, получим точку 3 (рисунок 11 а). Чтобы построить еще три точки на диагоналях квадрата, нужно через точку 3 провести прямые параллельные сторонам квадрата до пересечения с диагоналями, получим четыре точки (рисунок 11 б). Еще четыре точки находятся в точках пересечения горизонтальной и вертикальной прямых со сторонами квадрата. Соединим построенные точки, получим изображение окружности (рисунок 12).

а	б

а – построение точек А, В, С ; б – построение точек 1 и 2

Рисунок 10 – Этапы построения окружности

а	б

а – построение точки D; б – нахождение характерных точек

окружности на диагоналях квадрата

Рисунок 11 – Этапы построения окружности

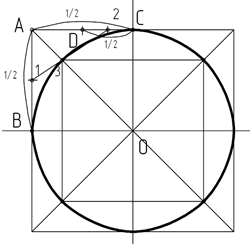
Рисунок 12 – Заключительный этап построения окружности