Рисование правильных многоугольников в аксонометрических проекциях

В техническом рисовании для выполнения наглядного изображения геометрических тел, их комбинаций, а также различных предметов необходимо сначала научиться строить плоские изображения многоугольников на основе аксонометрии. Рисование плоских фигур было рассмотрено в пункте 1.2. Перейдем к построению этих фигур в прямоугольной изометрической проекции.

Рассмотрим выполнение технического рисунка правильного треугольника в прямоугольной изометрии на осях zх. Так как при построении любых изображений в аксонометрических проекциях необходимо учитывать значение коэффициента искажения по осям, то будем ориентироваться на изображение треугольника в плоскости (двумерное пространство) (рисунок 15).

Далее необходимо провести оси х, y и z, как это было рассмотрено ранее (рисунок 13 б). Так как построения будут проводиться в плоскости, образованной осями zх, то необходимо наметить положение исходных прямых параллельно заданным осям. Основание треугольника расположим параллельно оси х, а высоту – параллельно оси z. Для построения вертикальной прямой (высоты треугольника) необходимо отступить от оси z произвольное расстояние, но не меньше половины основания треугольника (рисунок 16).

Рисунок 15 – Изображение правильного треугольника

на плоскости

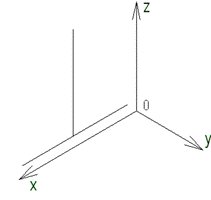
Рисунок 16 – Первый этап построения треугольника

Затем от точки пересечения проведенных прямых влево и вправо на прямой параллельной оси х откладывают по три отрезка той же длины, что и на исходном рисунке, а на вертикальной прямой – пять таких отрезков (длина единичного отрезка не меняется, т. к. коэффициенты искажения по осям равны единице). Соединив построенные точки, получим изображение правильного треугольника в прямоугольной изометрической проекции в плоскости, образованной осями х и z, т. е. во фронтальной плоскости проекций (рисунок 17).

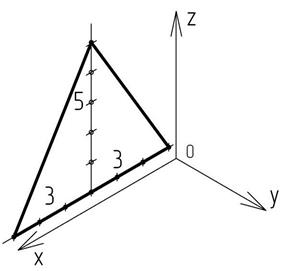
Рисунок 17 – Изображение правильного треугольника

в прямоугольной изометрической проекции

во фронтальной плоскости

Аналогично выше изложенным построениям можно построить правильный треугольник в оставшихся плоскостях: горизонтальной (образованной осями х и y) и профильной (образованной осями z и y) (рисунок 18). При этом основание треугольника и его высота должны быть проведены параллельно указанным осям, а единичные отрезки равны.

Рисунок 18 – Изображение правильного треугольника

в прямоугольной изометрической проекции

Построим правильный шестиугольник в прямоугольной изометрической проекции в плоскости, образованной осями х и y, опираясь на последовательность построения шестиугольника в плоскости (двумерное пространство) (рисунок 19).

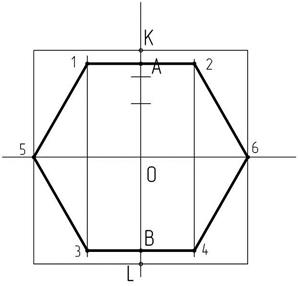
Рисунок 19 – Изображение правильного шестиугольника

на плоскости

Проведем оси х, у, z под углом 120º друг к другу, отложив на горизонтальной прямой пять единичных отрезков, а вниз на вертикальной прямой – три единичных отрезка (рисунок 20 а). Затем проведем прямые, параллельные осям х и у на таком расстоянии, чтобы построить на них параллелограмм (изображение квадрата), в котором будем проводить построения шестиугольника. Это расстояние должно быть чуть больше половины длины стороны квадрата (рисунок 20 б).

От точки пересечения прямых отложим отрезки, равные длине отрезка [05], полученные точки обозначим согласно рисунку 19 5, 6, К, L. Через них проведем прямые, параллельные заданным осям, получим параллелограмм (рисунок 21).

Затем отрезки прямой (56) поделим пополам, получим точки М и N, проведем через них прямые, параллельные оси оу (рисунок 22).

а	б

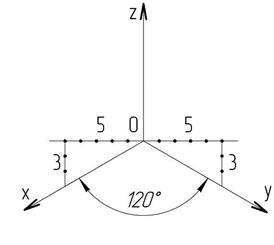
а – построение осей прямоугольной изометрической проекции;

б – построение центра параллелограмма

Рисунок 20 – Этапы построения шестиугольника

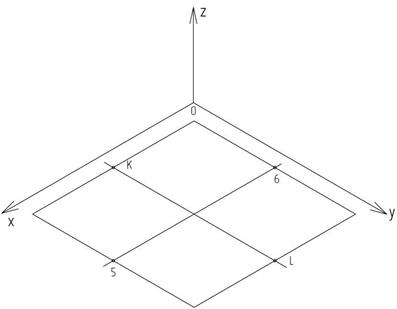
Рисунок 21 – Построение параллелограмма

Обозначим точку пересечения начальных прямых О^/ и разделим отрезок О^/К пополам, затем половину полученного отрезка еще раз пополам и 1/4 полученного отрезка еще раз пополам. Получим точку А, через которую нужно провести прямую, параллельную оси ох, до пересечения с прямыми, проходящими через точки М и N. Таким образом, построены точки 1, 2, 3, 4 (рисунок 23). Соединим построенные точки, получим изображение правильного шестиугольника в горизонтальной плоскости.

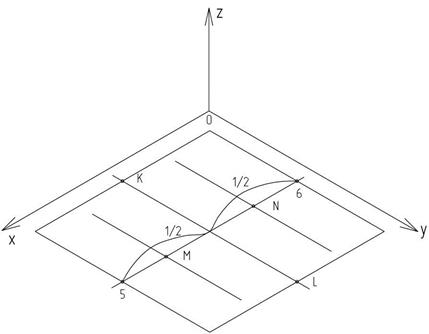
Рисунок 22 – Деление отрезков на равные части

Аналогично выше изложенным построениям можно построить правильный шестиугольник в оставшихся плоскостях: фронтальной (образованной осями х и z) и профильной (образованной осями z и y) (рисунок 24). При этом прямые, проходящие через точку О^/, должны быть проведены параллельно указанным осям.

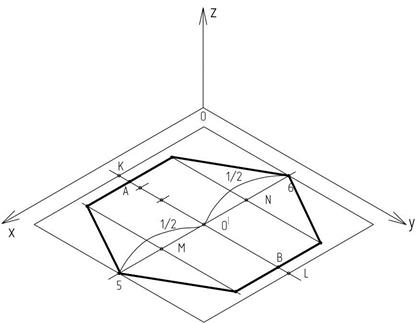
Рисунок 23 – Изображение правильного шестиугольника

в горизонтальной плоскости

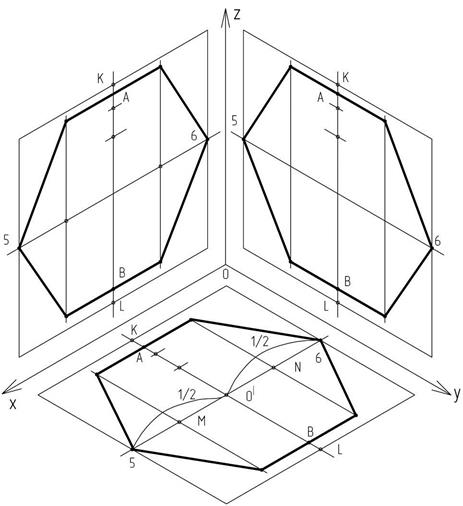
Рисунок 24 – Изображение правильного треугольника

в прямоугольной изометрической проекции

Рассматривая построение правильных многоугольников в косоугольной фронтальной диметрической проекции, нужно иметь в виду, что коэффициент искажения по оси оу равен 0,5. Это значит, что исходные размеры предмета, откладываемые вдоль оси оу, нужно уменьшать в два раза.

На рисунках 25, 26 показано построение правильного треугольника и правильного шестиугольника соответственно в косоугольной фронтальной диметрической проекции.

Рисунок 25 – Построение правильного треугольника в косоугольной фронтальной диметрической проекции

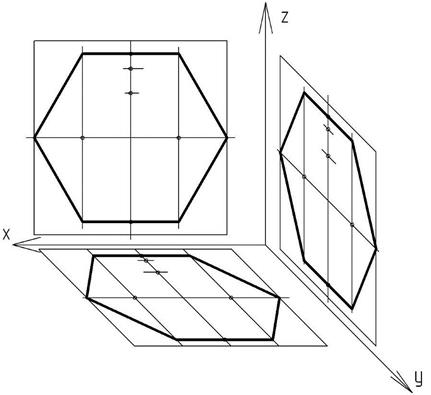
Рисунок 26 – Построение правильного шестиугольника

в косоугольной фронтальной диметрической проекции