Рисование геометрических тел и их комбинаций

Аксонометрическое рисование геометрических тел нельзя считать рисованием с натуры. В действительности мы видим все предметы с некоторой определенной точки зрения, тогда как в аксонометрии предметы изображаются условно, а точка зрения располагается в бесконечности.

Для рисования призмы в прямоугольной изометрии необходимо в горизонтальной плоскости на осях х и у построить параллелограмм, длина стороны которого равна длине стороны квадрата, и шестиугольник способом, описанным ранее в пункте 1.4. Затем на оси оz нужно отложить расстояние, равное высоте призмы, и повторить построение шестиугольника в параллельной плоскости, после чего нужно соединить вершины шестиугольников (рисунок 31). Если необходимо показать вырез ¼ части поверхности призмы, то нужно отметить точки, находящиеся на пересечении сторон шестиугольника с осями, и соединить их при помощи вертикальных прямых. Нанесение штриховки в прямоугольной изометрии выполняется по следующему правилу. От точки О на осях х, у, z нужно отложить равные расстояния (или провести окружность произвольного радиуса с центром в точке О), соединить построенные и точки и параллельно полученным отрезкам нанести линии с интервалом 3-4 миллиметра (рисунок 32).

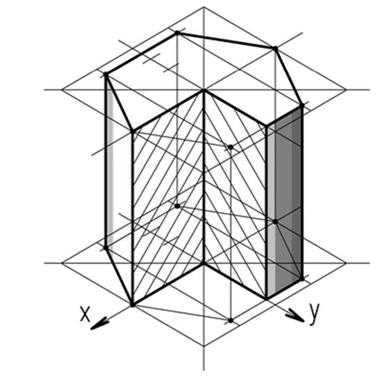
Рисунок 31 – Построение призмы

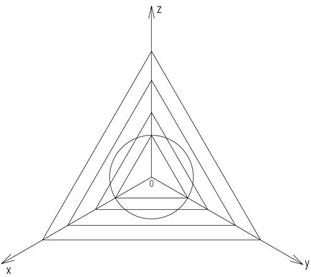
Рисунок 32 – Нанесение штриховки в прямоугольной изометрии

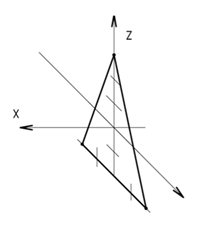
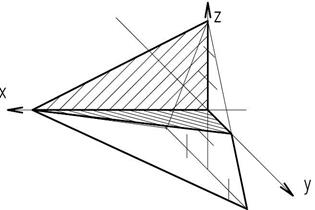
Для построения, например, пирамиды в косоугольной фронтальной диметрической проекции нужно задать оси, наметить положение основания. Если в основании пирамиды находится правильный треугольник, то его лучше построить, как показано на рисунке 33. Затем на оси ох отложить высоту пирамиды, соединить вершину пирамиды с вершинами ее основания и выполнить вырез (рисунок 34). Для выполнения штриховки нужно помнить, что коэффициент искажения по оси оу равен 0,5, поэтому по осям ох и оz откладывают равные расстояния, а по оси оу в два раза меньше. Полученные точки соединяют и параллельно намеченным линиям проводят штриховку (рисунок 35).

Рисунок 33 – Построение основания пирамиды	Рисунок 34 – Построение пирамиды

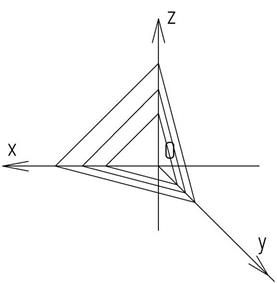
Рисунок 35 – Нанесение штриховки в косоугольной фронтальной

диметрической проекции

Рассмотрим построение цилиндра. Проекциями окружностей верхнего и нижнего основания цилиндра будут эллипсы. Нарисовав основания цилиндра на расстоянии, равном высоте цилиндра, проводят касательные образующие, при необходимости выполняют вырез (рисунок 36). Для построения конуса следует от центра эллипса вдоль оси оу (рисунок 37) отложить высоту конуса и провести касательные к эллипсу.

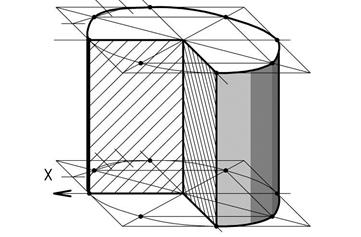
Рисунок 36 – Изображение цилиндра во фронтальной диметрии

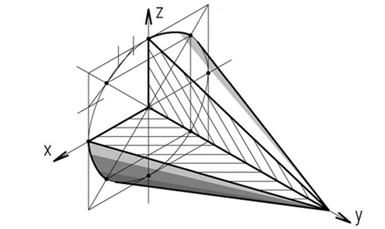
Рисунок 37 – Изображение конуса в прямоугольной изометрии

Для построения шара в прямоугольной изометрии необходимо построить три эллипса, находящихся в разных плоскостях, но имеющих один центр. Очерковая окружность, проведенная к построенным эллипсам, задаст контур шара (рисунок 38). Можно построить шар с частью выреза. На рисунке 39 дано изображение шара с вырезом 1/8 части.

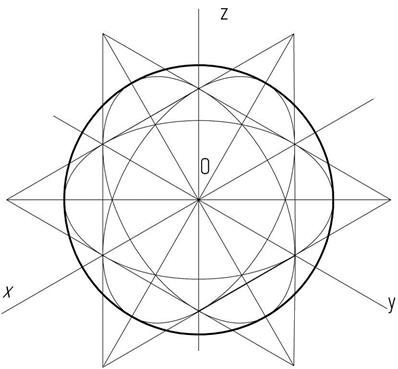
Рисунок 38 – Изображение шара в прямоугольной изометрии

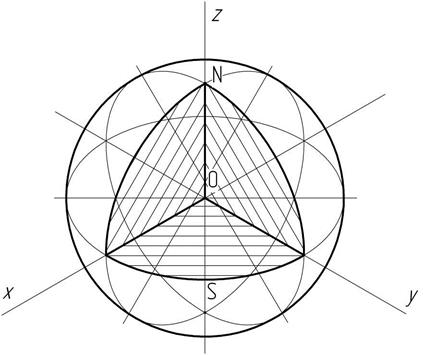
Рисунок 39 – Изображение шара с вырезом 1/8 части

При изображении пересекающихся цилиндров (рисунок 40) главные точки кривой находят построением в глазомерном масштабе. На рисунке показано построение главных точек кривой 1, 2, 3, 4 и промежуточных 5, 6, 7, 8 с помощью плоскостей-посредников, параллельных осям цилиндров.

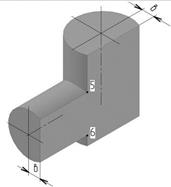
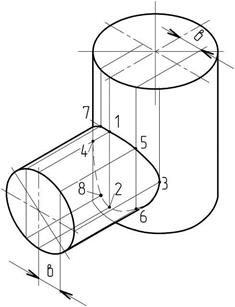
Рисунок 40 – Изображение пересекающихся цилиндров

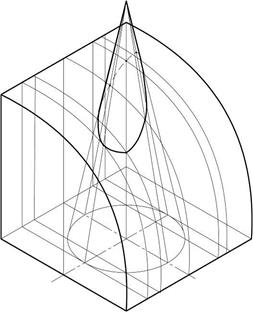
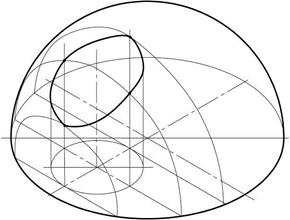
На рисунке 41 а показана линия пересечения цилиндрической поверхности с конусом, а на рисунке 41 б – линия пересечения цилиндра с шаровой поверхностью.

а	б

а – взаимное пересечение цилиндра с конусом; б – взаимное пересечение цилиндра со сферой

Рисунок 41 – Взаимное пересечение поверхностей вращения

Рассмотрим построение группы тел в прямоугольной изометрии (рисунок 42). Группа тел состоит из базового куба, на верхней грани которого построен усеченный конус, на левой грани – цилиндр, а на правой – призма. Причем все геометрические тела имеют сквозные отверстия.

Построим базовый куб. Для построения куба продлим оси х и у в обе стороны от начала координат. Замкнем контур куба так, чтобы он представлял собой правильный шестиугольник, а его большие диагонали образовывали равнобедренный треугольник. На левой грани куба построим цилиндр. Основание цилиндра – окружность, которая изображается в виде эллипса, будет вписана в левую грань куба. Второе основание необходимо построить на некотором расстоянии от первого эллипса, отложив на оси ох высоту цилиндра.

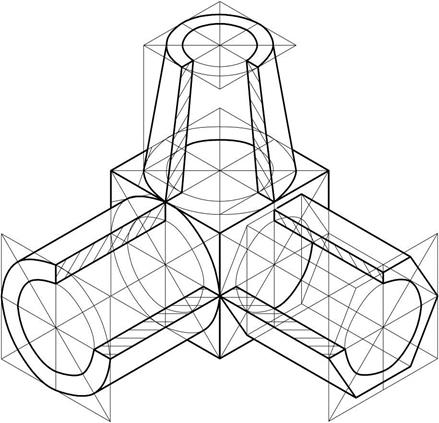
Рисунок 42 – Группа геометрических тел

Далее нужно соединить между собой два эллипса касательными, параллельными оси ох, получим контур цилиндра. Затем нужно построить отверстие. Так как отверстие цилиндрической формы, то необходимо нарисовать еще два эллипса и соединить их по касательным.

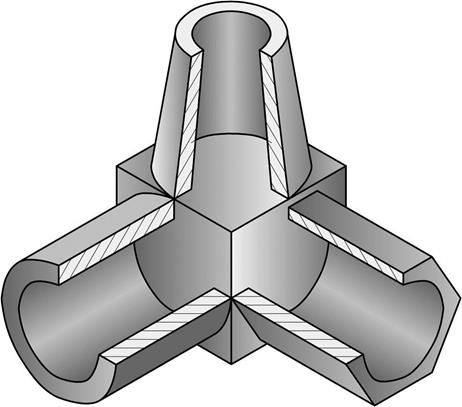
Рисунок 43 – Нанесение светотени на группу геометрических тел

На правой грани куба находится шестигранная призма. Построение шестиугольника было описано выше. Высоту призмы возьмем равной высоте цилиндра. Отложив ее длину на оси оу, получим центр параллелограмма – второго основания призмы, в который нужно вписать шестиугольник. Соединив вершины шестиугольника, получим контур призмы. Затем в призме нужно выполнить сквозное цилиндрическое отверстие. На верхней грани куба находится усеченный конус. В эту грань необходимо вписать эллипс, затем на оси z отложить расстояние, равное высоте усеченного конуса, получим центр второго основания. Построим малый эллипс и соединим его с помощью касательных с первым, получим контур усеченного конуса. Осталось построить отверстие. Для этого нужно нарисовать еще два эллипса, центры которых совпадают с центрами первых эллипсов и соединить их между собой по касательным. Выполнение выреза осуществляется аналогично выше изложенным построениям. Осталось нанести светотень на построенные поверхности (рисунок 43). В приложении представлены графические работы студентов, выполненные по данной теме.