Насадных инструментов

<1 234 5 6 7 >

Диаметр оправки оказывает большое влияние на работу РИ, например фрезы, т.к. она находится под действием крутящего и изгибающего моментов, поэтому необходимо выполнять проверочный расчет на прочность

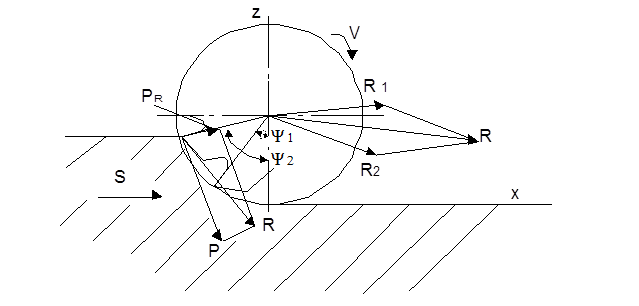
Рис. 3 Силы, действующие на зуб прямозубой фрезы

На зуб прямозубой фрезы действует окружная сила Р, касательная к траектории движения точки ее приложения, и радиальная сила Р_R направленная по радиусу. Равнодействующая этих сил R вызывает М_изг.

Сила Р зависит от удельной силы резания ри сечения снимаемой стружки Р = рf.

f = Ba_xsiny_x;

p = Ca^k_x = CS^k_z sin^ky_x;

P = CBS_z^k⁺¹sin^k⁺¹y_x ,

где: В - ширина фрезерования, мм; a_x - толщина среза, мм; S_z - подача на зуб, мм/зуб; y_x - угол поворота от начального до мгновенного положения зуба( с z = 1, y_x = j , угол контакта); С - коэфициент учитывающий свойства обрабатываемого материала и переднего углаg; k - показатель степени, учитывающий свойствава материала, износ фрезы и влияние СОЖ.

Если в процессе резания участвует несколько зубьев

Р_сум= СBS_z^k⁺¹S^zi₁[sin^k⁺¹y₁+ sin^k⁺¹y₂ +...+ sin^k⁺¹y_i],

где y₁,y₂ , ..., y_i - углы поворота соответствующих зубьев от начала фрезерования. Зная Р_сум можно определить суммарный крутящий момент.

M_d = P_сумD/2

Оправка находится под действием изгибающего момента, равного сумме двух моментов: M_bR_–от равнодействующей силы R_сум_,сил Р_сум и Р_r_сум, действующих в плоскости xz, причем

R_сум = ÖР²_сум + Р²_R_сум;

М_b_{Ро —}от осевой силы Р_{о сум}, действующей в плоскости ху, где Р_о_сум = R_сумtgw, где w - угол наклона винтовых зубьев.

Следовательно, M_b = M_bR ± M_bPo, (знак (+) - если осевая сила направлена к шпинделю, (-) - от шпинделя).

Изгибающий момент от силы R

M = Rl = (3/16 - 1/4) RL,

где l - расстояние между точками приложения силы R и максимального изгибающего момента, L - расстояние между опорами, мм

Изгибающий момент от силы Р_осум:

M_bPo = P_осум D/2 = P_сумtgwD/2.

Ориетировочно считается

Р_осум = (0,4¸0,6) Р_сум

Расчетный момент по IV теории прочности М_расч= Ö М²_b +M²_d.

По расчетному моменту и определяется диаметр оправки

d_o = ÖM_расч/s_в×0,1

Полученный диаметр оправки округляется в большую сторону.

Крепление РИ при помощи конического хвостовика.

Большинство концевых инструментов закрепляется в шпинделе станка при помощи хвостовика с наружным конусом и лапкой или резьбовым отверстием.

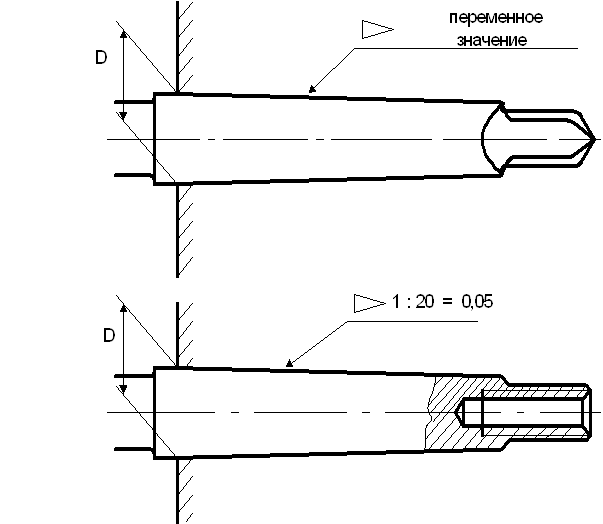
Рис. 4 Типы конических хвостовиков: а) конус Морзе, б) метрический конус

Копуса Морзе №0 имеет D = 9,045 мм,

конусность 1: 19,212 = 0,05205;

№1 = 12,065; 1: 20,047 = 0,04988;

№2 = 17,79; 1: 20,020 = 0,049995;

№3 = 23,825; 1: 19,922 = 0,0502;

№4 = 31,267; 1: 19,254 = 0,055194;

№5 = 44,399; 1: 19,002 = 0,05263;

№6 = 63,348; 1: 19,180 = 0,05214

Метрические конуса D = 4,6,80,100, 120, 160, 200 мм, конусность 1:20 = 0,05.

Конус служит для передачи крутящего момента от шпинделя станка к РИ. Передача осуществляется в результате трения контактирующих поверхностей, возникающего в процессе резания под действием осевой силы. Крутящий момент должен передаваться только конусом без участия лапки, которая служит только для выталкивания клином.

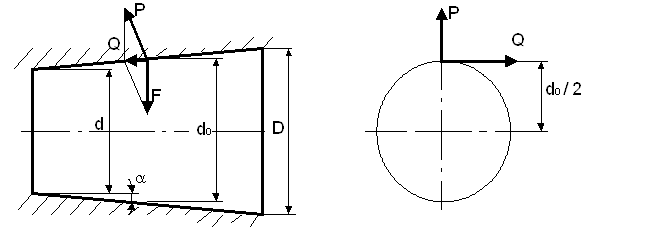
Рис. 5 Силы, действующие на боковой поверхности конического хвостовика

Осевую силу можно разложить на две составляющие: Р - перпендикулярную к поверхности конуса и F - ^ к оси сверла.

Р = Q/sina.

Крутящий момент определяется по формуле

М = mРd_o/2 = m(Q/sina)(D+d)/4,

где D и d - max и min диаметры рабочей части конуса, мм; m - коэф. трения (0,096); Q - осевая сила, Н; mР - сила трения, Н.

Эта формула справедлива при условии, угол a - точно выдержан в обеих сопрягаемых поверхностях шпинделя и сверла. На практике погрешность D (суммарная) в угле a не превышает 10’.

Тогда крутящий момент выразится

М = (mQ/sina)(D+d)/2(1-0,04Da),

где Da = 0-10’.

Для спирального сверла существует зависимость между М и Q. Так для стали с s_в = 300¸1100 МПа М/Q = (0,038¸0,025)d; для чугуна средней твердости М/Q = 0,034d; где d - диаметр сверла. При расчете необходимо брать М/Q = max.