И его применение к различным процессам

Первый закон термодинамики является количественной формулировкой всеобщего закона сохранения энергии применительно к процессам, связанным с превращениями теплоты и работы. Он утверждает, что в любой изолированной системе запас энергии остается постоянным.

Первый закон термодинамики возник в эпоху создания тепловых двигателей. С появлением тепловых машин перед человечеством встала естественная задача создания экономически выгодных машин. Предпринимались многочисленные попытки создания вечного двигателя I рода − тепловой машины, производящей работу без затрат энергии.

Невозможно создать вечный двигатель I рода − это утверждение также является одной из формулировок первого закона термодинамики.

Необходимо отметить, что первый закон термодинамики представляет собой постулат − он не может быть доказан логическим путем или выведен из каких-либо более общих положений. Истинность этого закона подтверждена многолетним опытом человечества.

Первый закон термодинамики устанавливает связь между теплотой Q, работой А и изменением внутренней энергии системы DU.

Q

Пусть к закрытой системе подведено некоторое количество теплоты Q. Согласно первому закону термодинамики эта теплота идет в общем случае на увеличение внутренней энергии и на совершение системой работы:

Q = DU + A. (1.2)

Для бесконечно малых величин

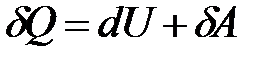. (1.3)

Знак d в уравнении (1.3) отражает тот факт, что теплота и работа − функции процесса и их бесконечно малое изменение не является полным дифференциалом.

В уравнениях (1.2) и (1.3) используется термодинамическая система знаков: теплота положительна, если она передается системе; работа положительна, если она совершается системой.

В общем случае работа является суммой нескольких качественно различных видов работ (механической, электрической, магнитной, поверхностной и др.). Принято все виды работ за исключением работы расширения (сжатия) называть полезной работой 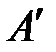. С учетом этого первый закон термодинамики примет вид:

.

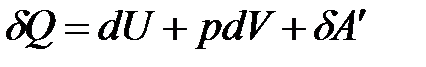Если совершается только работа расширения (сжатия) pdV, то

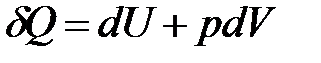. (1.4)

Рассмотрим простейшую термодинамическую систему – газ, находящийся в цилиндре с поршнем. При подводе к нему теплоты Q газ нагревается (следовательно, увеличивается его внутренняя энергия) и расширяется (совершается работа). Таким образом, теплота расходуется частично на увеличение внутренней энергии и частично на совершение работы против внешних сил.

Применим уравнение (1.4) для анализа основных термодинамических процессов.

1) Изохорный процесс (V = const, dV = 0). Так как работа расширения при этом равна 0, то, очевидно, что вся теплота, подведенная к системе, идет на увеличение внутренней энергии:

,

.

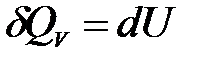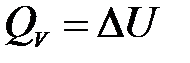Таким образом, теплота изохорного процесса равна изменению внутренней энергии и, следовательно, является функцией состояния.

2) Изобарный процесс (p = const, dp = 0).

Уравнение (1.4) в этом случае запишется в виде

,

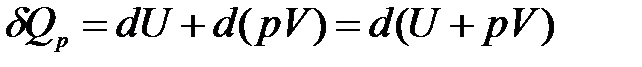где U + pV = H − функция состояния системы, называемая энтальпией.

,

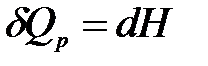Q_p = DH.

Таким образом, теплота изобарного процесса равна изменению энтальпии и является функцией состояния.

Получим формулу для расчета работы расширения, совершаемой в изобарном процессе.

dА = pdV.

Проинтегрируем в интервале от V₁ до V₂:

.

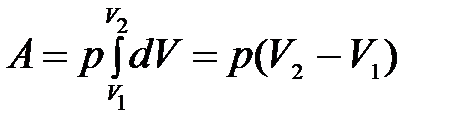Для изобарного процесса, протекающего в идеальном газе, в соответствии с уравнением Менделеева-Клапейрона (1.1) для начального и конечного состояния

,

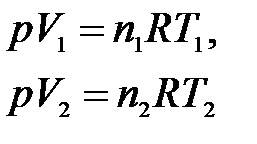работа расширения равна

.

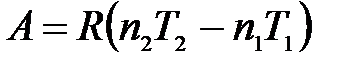Если протекает изобарно-изотермический процесс (р, Т = const), уравнение принимает вид:

,

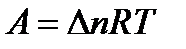где .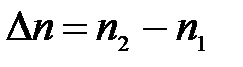

Связь между Q_V и Q_p определяется уравнением:

.

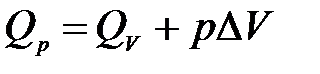Для реакций, протекающих с участием только конденсированных фаз, объем системы практически не изменяется (DV = 0) и Q_p» Q_v. Для реакций, протекающих с участием веществ в газообразном состоянии, в том числе идеальных и реальных газов при невысоких давлениях, к которым применимо уравнение Менделеева-Клапейрона, изменение объема вызвано уменьшением или увеличением числа моль газообразных компонентов в системе

,

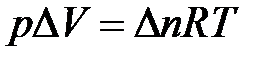где Dn – изменение числа моль газообразных продуктов реакции и исходных веществ:

.

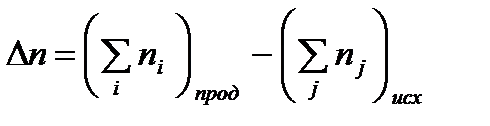Следовательно,

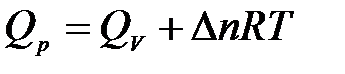
или .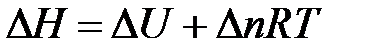

3. Изотермический процесс (Т = const)

Рассмотрим изотермический процесс, протекающий в идеальном газе. Согласно закону Гей-Люссака-Джоуля внутренняя энергия идеального газа зависит только от температуры и не зависит от давления и объема. Это значит, что при
Т = const ΔU = 0. Следовательно, для идеального газа в изотермическом процессе работа совершается только за счет поглощаемой теплоты

.

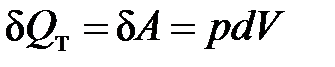Для идеального газа в соответствии с уравнением (1.1)

,

.

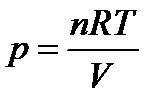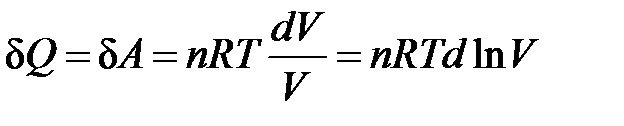После интегрирования

.

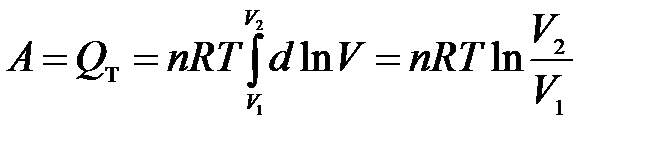При Т = const

,

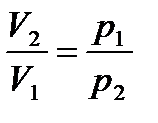тогда

.

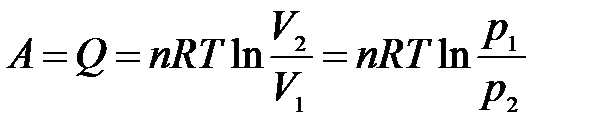4) Адиабатический процесс осуществляется без теплообмена с окружающей средой (dQ = 0).

dA = − dU,

A = − DU.

В адиабатическом процессе работа может совершаться только за счет убыли внутренней энергии.

Термохимия

Термохимия – раздел химической термодинамики, изучающий взаимосвязь химических и физико-химических процессов с сопровождающими их тепловыми эффектами.

Тепловой эффект – это количество теплоты, которое система выделяет или поглощает в необратимо протекающем процессе.

В любом акте химического превращения принимает участие некоторая совокупность атомов, характеризующая исходные вещества, а после их перераспределения – и продукты реакции. Перегруппировка атомов вызвана изменением химических связей в молекулах реагирующих веществ. Поскольку внутренняя энергия исходных молекул отличается от внутренней энергии продуктов реакции, то происходит изменение внутренней энергии системы, которое сопровождается тепловым эффектом и совершением работы.

Процессы, при протекании которых теплота выделяется, являются экзотермическими. Процессы, протекающие с поглощением теплоты, – эндотермические.