Модели на основе методов статистических решений

Один из подходов к диагностированию заключается в использовании так называемых статистических решений. При этом решающее правило выбирается исходя из некоторых условий оптимальности, например, из условия минимального риска. Рассмотрим технологию распознавания при наличии одного диагностического параметра.

Пусть производится диагностирование трансформатора по выделению газа из масла (параметр k). Задача состоит в выборе значения k₀ параметра k таким образом, что при k > k₀ следует принимать решение о прекращении эксплуатации трансформатора, а при k < k₀ - допускать дальнейшую эксплуатацию. Разделение производится на два класса: D₁ - исправное состояние; D₂ - наличие дефекта. Тогда указанное решающее правило означает:

при 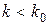; ; 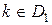при ;

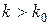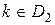
Выделение газа неоднозначно характеризует состояние масляного трансформатора (масло имеет собственный запах, содержание газов не превышает допустимых пределов и т.д.). Плотность распределения k для дефектных и исправных трансформаторов показана на рисунке 8.

Области исправного (D₁) и дефектного (D₂) состояний пересекаются и поэтому принципиально невозможно выбрать значение k₀, при котором не было бы ошибочных решений. Задача состоит в том, чтобы выбор k₀ был в некотором смысле оптимальным, например, давал бы наименьшее число ошибочных решений.

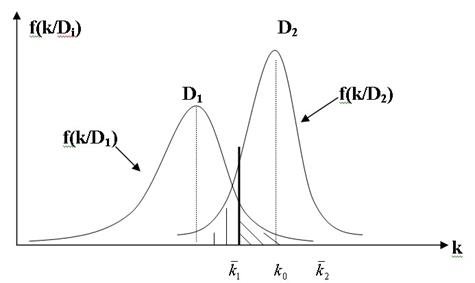
Рис. 8. Распределение плотности диагностического параметра

k для исправного D₁ и дефектного D₂ состояний

Возможными ошибками при принятии решений являются: ложная тревога (ошибка первого рода), когда исправный объект признается дефектным (вместо D₁ считают, что имеет место D₂), и пропуска дефекта (ошибка второго рода), когда объект, имеющий дефект признается исправным (вместо D₂ признается D₁).

Обозначим через H_ij (ij = 1, 2) возможные ошибки, где i - соответствует индексу принятого диагноза, а j - индексу действительного состояния. Тогда H₁₂ - это пропуск дефекта, а H₂₁ - ложная тревога.

Вероятность ложной тревоги равна вероятности произведения двух событий: наличия исправного состояния и значения k > k₀ для исправного состояния:

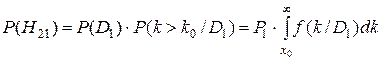
где P₁ = P(D₁) - априорная вероятность диагноза D₁ (считается известной на основе предварительных статистических данных).

Вероятность пропуска дефекта определяется аналогично:

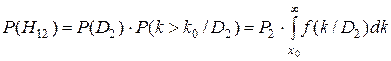
Ошибочное решение слагается из вероятности ложной тревоги и вероятности пропуска дефекта. Если приписать цены этим ошибкам (C₂₁ - стоимость ложной тревоги, а C₁₂- стоимость пропуска дефекта), то получим искомое общее выражение для вычисления среднего риска:

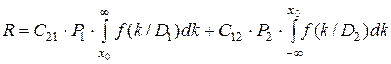. (3.12)

3.2.1. Методы минимального риска, минимального числа ошибочных

решений, наибольшего правдоподобия

Граничное условие k₀ находится из условия минимального среднего риска. Дифференцируя (3.12) по k₀ и приравнивая производную нулю, получим условие экстремума

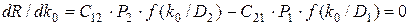, (3.13)

тогда отношение правдоподобия будет иметь вид:

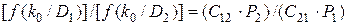. (3.14)

Это условие часто определяет два значения k₀, из которых одно соответствует минимуму, а второе - максимуму риска. Для существования минимума R в точке k = k₀ вторая производная должна быть положительной, то есть

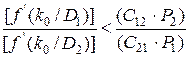. (3.15)

Для одномодальных распределений (содержащих не более одного максимума) при 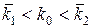условие (3.15) выполняется.

В соответствии с (3.14) правило решения по методу минимального риска имеет вид:

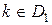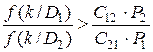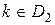при ,

при .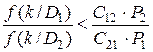

Рассмотрим случай, когда параметр k имеет нормальное распределение при исправном D₁ и неисправном D₂ состояниях и σ₁ = σ₂ = σ. При этом плотности распределений будут иметь следующий стандартный вид:

,

.

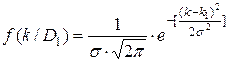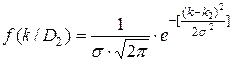Подставив эти соотношения в (3.14), прологарифмировав и упростив получим:

.

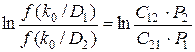Откуда получаем выражение для расчета k₀:

.

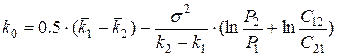При k < k₀, принимается решение 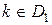. При k > k₀, принимается решение .

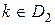Частным случаем рассмотренного метода является метод минимального числа ошибочных решений. Эти методы эквивалентны, если стоимости решений одинаковы. При данном методе для одномодальных распределений решение 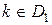принимается при условии, что

,

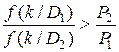а решение 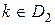принимается при условии, что

.

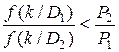Метод наибольшего правдоподобиятакже является частным случаем метода минимального риска. Правило решения имеет следующий вид:

принимаетсяk 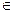D₁, если ,

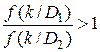где k - значение диагностического параметра.

Граничное значение находится из условия

.

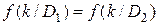Сопоставляя уравнения (3.14) и (3.15) видно, что они совпадают, если допустить, что

.

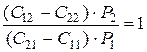Примечание. При C₂₂ = C₁₁ = 0 допущение упрощается:

.

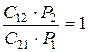Метод минимакса

Этот метод предназначен для ситуации, когда отсутствуют предварительные статистические сведения о вероятности диагнозов D₁ и D₂. Рассматривается «наихудший случай», то есть наименее благоприятные значения P₁ и P₂, приводящие к наибольшему значению (максимуму) риска.

Величина риска зависит отk₀ и P₁ (вероятность второго диагноза P₂ = 1 - P₁), в частности

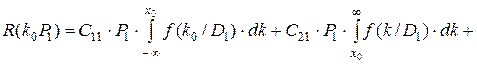
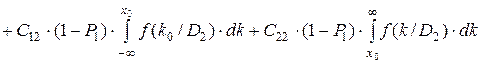. (3.16)

здесь C₁₁ и C₂₂ - стоимости правильных решений.

Для нахождения экстремума уравнение (3.16) преобразуют (приравнивают частные производные по k₀ и P₁ к нулю). Условие dR/dk₀ = 0 дает

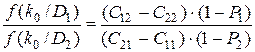. (3.17)

Условие dR/dP₁ = 0 дает

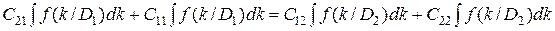. (3.18)

Значения k₀ и P₁, являющиеся корнями уравнений (3.17) и (3.18), определяют экстремальную точку R(k₀, P₁). Для одномодальных распределений величина риска становится минимальной (то есть минимальной среди максимальных значений, вызванных «неблагоприятной» величиной P₁). По методу минимакса выбирают величину k₀таким образом, чтобы при наименее благоприятных значениях P₁ потери, связанные с ошибочным решением, были минимальными.

Опуская процедуры точного решения уравнений (3.17) и (3.18) (например, с помощью метода Ньютона) представим приближенные решения. Так, в первом приближении можно принять, что 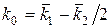. Тогда из (3.17) находим наименее благоприятное значение вероятности исправного P^*₁ и неисправного P^*₂ состояний:

,

.

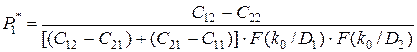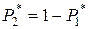Величину риска определяем из равенства (3.16) при значениях k = k^*₀, P₁ = P^*₁. Вероятность ложной тревоги и пропуска дефекта может быть найдена из соотношения

,

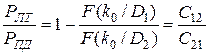где 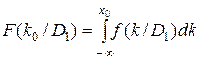- функция распределения D₁ (в общем виде);

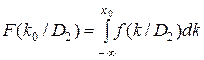- функция распределения D₂ (в общем виде).