Метод Неймана-Пирсона

В случае если неизвестны оценки стоимости ошибок, решается задача минимизации одной ошибки при определенном (допустимом) уровне другой. По методу Неймана-Пирсона минимизируется вероятность пропуска дефекта при заданном допустимом уровне вероятности ложной тревоги.

Вероятность ложной тревоги

,

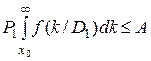где A - заданный допустимый уровень ложной тревоги; P₁- вероятность исправного состояния.

На рисунке 8 видно, что увеличение ошибки ложной тревоги (сечение k₀ перемешается влево) приводит к уменьшению величины ошибки пропуска дефекта. Ее наименьшее значение достигается при

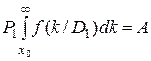. (3.19)

В практических задачах можно принимать A = r∙P₂, где r - коэффициент избыточности, зависящий от разрешающей способности диагностических средств, опасности дефекта, экономических затрат и других соображений.

При дефектах с ограниченными последствиями можно принять r = 1…3. При опасных дефектах r = 3…10. Для редко встречающихся (P₂ < 0.01), но крайне опасных дефектов, коэффициент избыточности r может достигать и больших значений.

В задачах диагностики можно использовать и другой подход: определить значение k₀ исходя из выбранной вероятности пропуска дефекта. В этом случае

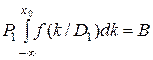. (3.20)

где B - заданное значение вероятности пропуска дефекта, которое выбирается с учетом указанных соображений.

Если дефект крайне нежелателен даже на единичном объекте, то можно принять

,

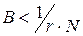где N - общее число объектов, находящихся в эксплуатации;r - коэффициент избыточности (1 ≤r ≤ 10).

Во всех случаях для реализации принципа невозможности маловероятных событий величина B должна быть малой (B ≤ 0.01). В методе Неймана-Пирсона граничное значение k₀ определяется из уравнения (3.19) или (3.20). При практическом решении таких уравнений целесообразно использовать метод Ньютона.