Диагностическая матрица

Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу, которая формируется на основе предварительного статистического материала. В таблице содержатся вероятности разрядов признаков при различных диагнозах. Если признаки двухразрядные (да - нет), то в таблице достаточно указать вероятность появления признака 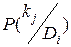. Вероятность отсутствия признака .

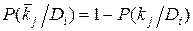В диагностическую матрицу включены априорные вероятности диагнозов.

Диагноз Di	Признаки kj
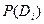
k1	k2	k3
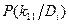
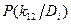
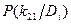
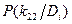
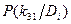
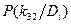
D1	0.8	0.2	0.1	0.1	0.2	0.8	0.3
D2	0.1	0.7			0.1	0.9	0.1
…	…	…	…	…	…	…	…

Поясним метод Байеса. Например, при наблюдении за трансформатором проверяются два признака: k₁ - повышение температуры обмоток трансформатора и k₂ - уровень шума, создаваемый трансформатором. Предположим, что появление этих признаков связано с неисправностью трансформатора. При нормальном состоянии трансформатора (состояние D₃) признак k₁ не наблюдается, а признак k₂ наблюдается в 5% случаев. На основании статистических данных известно, что 80% трансформаторов вырабатывает ресурс в нормальном состоянии, 5% имеют состояние D₁ и 15% - состояние D₂. известно также, что признак k₁ встречается при состоянии D₁ в 20%, а при состоянии D₂ в 40% случаев; признак k₂ при состоянии D₁ встречается в 30%, а при D₂ в 50% случаев. Сведем данные в диагностическую таблицу.

Di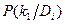
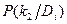
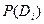
D1 D2 D3	0.2 0.4 0.0	0.3 0.5 0.05	0.05 0.15 0.80

Вероятность состояния, когда обнаружены оба признака определяем по формуле (3.11),

.

,

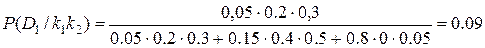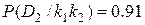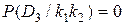
Признак k₁ отсутствует, присутствует признак k₂. Отсутствие признака k₁ есть признак наличия 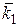(противоположное событие), причем .

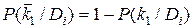Для расчета также применяют формулу (3.11), но 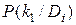заменяют на .

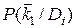Тогда .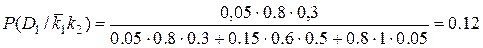

;

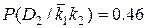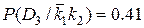
Когда отсутствуют оба признака,

.

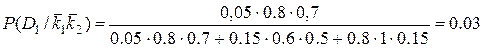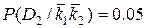
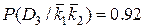
Из проведенных расчетов можно установить, что при наличии двух признаков в трансформаторе с вероятностью 0.91 имеется состояние D₂, т.е. увеличение шума. При отсутствии обоих признаков наиболее вероятно нормальное состояние (вероятность 0.92).Во втором случае, так как вероятности примерно одинаковы, необходимо дополнительное исследование для уточнения состояния трансформатора.

Решающее правило

Правило, в соответствии с которым принимается решение о диагнозе. В методе Байеса объект с комплексом признаков К^* относится к диагнозу с наибольшей (апостериорной) вероятностью.

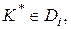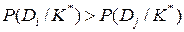если , (j=1,2,…n; )

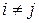Условие указывает, что объект, обладающий данной реализацией комплекса признаков К^*, принадлежит диагнозу (состоянию) D_i. Данное правило уточняется введением порогового значения для вероятности диагноза:

,

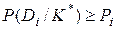где Р_i заранее выбранный уровень распознавания для диагноза D_i.

При этом вероятность ближайшего конкурирующего диагноза не выше 1-Р_i. Обычно принимается 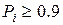. При условии 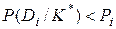решение о диагнозе не принимается (отказ от распознавания) и требуется поступление дополнительной информации.