МАТЕМАТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ В ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ

Тема 3. Статистические методы распознавания признаков

План лекции

3.1. Метод Байеса

3.1.1. Основы метода

3.1.2. Диагностическая матрица

3.1.3. Решающее правило

3.2. Модели на основе методов статистических решений

3.2.1. Методы минимального риска, минимального числа ошибочных

решений, наибольшего правдоподобия

3.3. Метод минимакса

3.4. Метод Неймана-Пирсона

3.5. Метод последовательного анализа

При наличии неопределенности принятия решения применяют специальные методы, учитывающие вероятностную природу событий. Они позволяют назначать границу поля допуска параметра или необходимое число опытов для принятия решения о диагностировании. Большая часть методов основана на том, что имеется некоторая доопытная вероятность в постановках диагностирования.

Так, большинство методов предполагают априорно известными вероятности диагностирования для однотипных объектов, находящихся в одинаковых условиях. Часто выбор того или иного решающего правила проводится на основе оптимизации по некоторым критериям. Статистические методы позволяют одновременно учитывать диагностические сигналы различной физической природы, так как они работают лишь с их вероятностными характеристиками.

Следует учитывать, что рассматриваемые методы принятия решений являются лишь инструментом, а окончательное решение, как и ответственность за его последствия, лежит на конкретном человеке.

Метод Байеса

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса, занимает особое место благодаря простоте и эффективности.

Имеет он и недостатки: большой объем предварительной информации, угнетение редко встречающихся диагнозов. Однако в случаях, когда объем статистических данных, позволяет применить метод Байеса, его целесообразно использовать как один из наиболее эффективных и надежных методов.

Основы метода

Метод основан на простой формуле Байеса. Если имеется диагноз D_i и простой признак k_j, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния D_i и признака k_j)

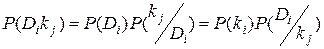. (3.1)

Из этого равенства вытекает формула Байеса

. (3.2)

Очень важно определить точный смысл всех входящих в эту формулу величин. 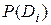- вероятность диагноза D_i, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у N_i объектов имелось состояние D_i, то

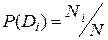. (3.3)

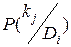вероятность появления признака k_j у объектов с состоянием D_i. Если среди N_i объектов, имеющих диагноз D_i у N_ij, проявился признак k_j, то

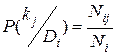. (3.4)

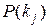- вероятность появления признака k_j во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак k_j был обнаружен у N_j объектов, тогда

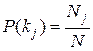. (3.5)

Для установления диагноза специальное вычисление 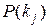не требуется. Как будет ясно из дальнейшего, значения 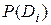, , 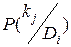известные для всех возможных состояний, определяют величину .

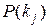В равенстве (3.2) 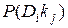- вероятность диагноза D_i после того, как стало известно наличие у рассматриваемого объекта признака k_j (апостериорная вероятность диагноза).

Обобщенная формула Байеса. Эта формула относится к случаю, когда обследование проводится по комплексу признаков K, включающему признаки k₁, k_2, …k_ν. Каждый из признаков k_j имеет m_j разрядов (k_j1, k_j2, …k_js, …, k_jmj). В результате обследования становится известной реализация признака 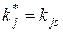и всего комплекса признаков K^*. Индекс * означает конкретное значение (реализацию признака). Формула Байеса имеет вид

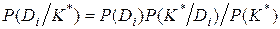, i=1, 2, …, n, (3.6)

где 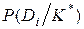- вероятность диагноза D_i после того, как стали известны результаты обследования по комплексу признаков К; 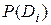- предварительная вероятность диагноза D_i (по предшествующей статистике).

Формула 3.6 относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний и потому

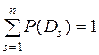. (3.7)

В практике нередко существуют несколько состояний A₁, …A_r, причем некоторые могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов D_i следует рассматривать отдельные состояния D₁=A₁,…D_r=A_r и их комбинации D_r+1=A₁^A₂, … и т.п.

Если комплекс признаков состоит из ν признаков, то

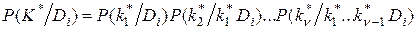, (3.8)

где 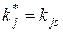- разряд признака, выявившийся в результате обследования.

Для диагностически независимых признаков

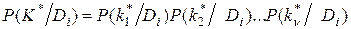. (3.9)

Вероятность появления комплекса признаков K^*

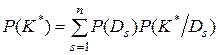. (3.10)

Обобщенная формула Байеса может быть записана

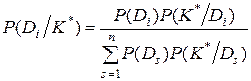, (3.11)

где 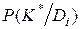определяется равенством 3.8 и 3.9.

Из соотношения 3.11 вытекает 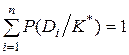, что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация двух диагнозов невозможна.