МАТЕМАТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ В ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ

Тема 2. Математические модели, задачи и алгоритмы технической

Диагностики

План лекции

2.3. Таблица функций неисправностей

2.4. Прямые и обратные задачи диагноза

2.5. Алгоритмы диагноза и средства диагноза

Таблица функций неисправностей

Совокупность функций (2.3) и (2.4) 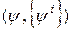можно представить в табличной форме.

Обозначим множество технических состояний объекта символом E. Пусть 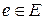обозначает его исправное состояние, а 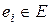- его i - неисправное состояние. Каждому i-му неисправному состоянию соответствует неисправность 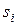из множества S, и наоборот.

Построим прямоугольную таблицу, в строках которой поставим элементарные проверки 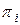из множества П, а в столбцах – технические состояния e из множества Е, или что тоже , функции 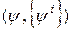, , 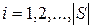реализуемые объектом, находящимся в исправном 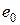или i-неисправном 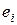состоянии. Значение индекса i=0 относится к столбцу исправного состояния e. На пресечении столбцов 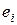и строк 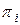таблицы проставим результат 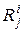элементарной проверки 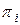объекта, находящегося в техническом состоянии 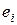. Множество всех результатов 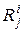, 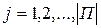; 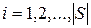обозначим символом R. Очевидно, 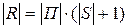. Построенную таблицу будем называть таблицей функций неисправностей объекта диагноза.

R	Е
е0	…		…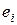
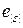
П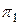
…
…

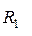
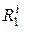
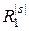
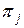
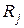
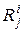
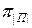
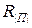
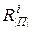
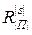
Непосредственное использование данной таблицы часто бывает затрудненно, по причине высокой размерности таблицы. Однако как универсальная математическая модель объекта диагноза она очень наглядна и удобна для процедур построения и реализации алгоритмов диагноза.

Можно заметить, что задание таблицы эквивалентно заданию системы функций (2.3) и (2.4). Столбец 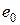задает поведение исправного объекта, т.е. функцию (2.3), а остальные ее столбцы – поведения неисправного объекта, т.е. функцию (2.4).

Для определенности примем, что множество П обладает свойством обнаружения неисправностей из множества S, т.е. для любой неисправности 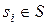найдется хотя бы одна элементарная проверка 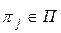, - такая, что 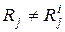, а также свойством различения всех неисправностей из множества S, т.е. для каждой пары неисправностей 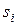, , 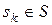, 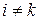найдется хотя бы одна элементарная проверка 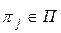, такая, что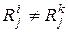

Как всякая математическая модель объекта диагноза таблица функций неисправностей нужна для построения алгоритмов диагноза и для построения физической модели объекта.

Изложим основные операции процесса построения алгоритма диагноза по таблице функций неисправностей.

Задание на построение алгоритма диагноза должно содержать сведения о требуемой глубине диагноза. Требуемую глубину диагноза можно задавать через фиксированное разбиение множества Е на 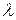непересекающихся подмножеств 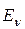, где ν=1,2, …, λ .

Тогда проверке исправности, работоспособности или правильности функционирования соответствует минимальная глубина диагноза, при которой λ=2., причем E₁={ 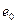} и E₂={ 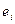}, i=1,2, ,…, |S|. При поиске неисправности с максимальной глубиной диагноза (т.е. с точностью до каждого одного технического состояния) λ=|S|+1; E₁={ 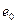}; E_ν={ 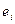}, i=1,2,…,|S|; ν=i+1. Промежуточные значения глубины диагноза характеризуются условием 2<λ<|S|+1.

Способ разбиения множества Е технических состояний объекта на подмножества 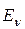является достаточно универсальным. Но он неудобен тогда, когда отсутствует соответствие такого разбиения разбиению объекта на конструктивные составные части. Значительно удобнее требуемую глубину диагноза задавать через разбиение множества конструктивных компонент объекта на непересекающиеся подмножества. Например, широко известно требование проведения диагноза с глубиной до сменного блока. Этот случай соответствует рассмотрению одиночных неисправностей объекта. Поэтому получаем λ=N+1, E₁={e₀}, E_ν=E_l. Где Е_l – подмножество технических состояний неисправностей каждого отдельного блока; N – количество сменных блоков, если в качестве последних принять неисправности каждого сменного блока. Иначе обстоит дело тогда, когда нельзя исключить возможность существования неисправности в нескольких блоках. В этом случае получаем 2^N-1 подмножеств технических состояний, т.е. (с учетом исправного состояния е) λ=2^N.

Основу любого алгоритма диагноза составляет совокупность (множество) П входящих в него элементарных проверок. Для того чтобы обеспечить требуемую глубину диагноза, эта совокупность должна различать каждую пару технических состояний, принадлежащих разным подмножествам Е_ν и Е_μ 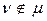, хотя может не различать любую пару технических состояний, принадлежащих одному и тому же подмножеству Е_ν. 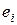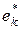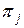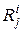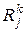Первое условие означает, что для каждой пары технических состояний , , принадлежащих разным подмножествам Е_ν и Е_μ, среди элементарных проверок совокупности П найдется хотя бы одна элементарная проверка , результаты и которой различны, т.е. 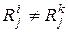. Совокупность П элементарных проверок алгоритма диагноза будем называть полной, если она обеспечивает проведение диагноза либо с заданной глубиной, либо с глубиной обеспечиваемой множеством П всех допустимых элементарных проверок. Совокупность П называется не избыточной, если удаление из нее одной элементарной проверки ведет к уменьшению глубины диагноза.

Построение по таблице функций неисправностей всех полных не избыточных совокупностей элементарных проверок П можно осуществить, выполнив 2 операции.

1. Просмотром всех возможных неупорядоченных пар столбцов таблицы выделить пары 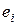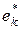технических состояний, принадлежащих разным подмножествам Е_ν и Е_μ, и для каждой такой пары просмотром (перебором) всех строк таблицы определить подмножества 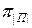элементарных проверок 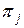результаты 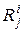и 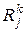которых для технических состояний 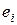, , 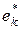различны.

2. Перебором всех подмножеств 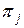, полученных в результате выполнения операции 1, найти все такие совокупности П элементарных проверок, чтобы в каждой из них для каждого подмножества 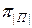нашлась хотя бы одна элементарная проверка 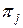, принадлежащая этому подмножеству .

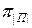Остановимся теперь на применении таблицы функций неисправностей при построении физической модели объекта в СД. Определение совокупности 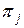элементарных проверок, входящих в алгоритм диагноза, соответствует выделению определенной совокупности строк таблицы функций неисправности. Подтаблицу, образованную совокупностью 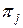строк, будем называть П-таблицей функций неисправностей. Нетрудно видеть, что П-таблица является заданием функций (2.6), (2.7), определяющих физическую модель объекта в средствах диагноза. При представлении физической модели объекта П-таблицей процесс расшифровки фактических результатов 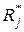элементарных проверок можно представить следующим образом. Каждая проверка выделяет строку П-таблицы, а ее фактический результат 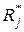делит множество столбцов таблицы на два подмножества. Те столбцы 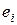, i=1,2,…|S|, для которых 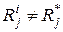, вычеркиваются из таблицы. Оставшиеся столбцы, для которых 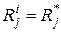, представляют подмножество возможных технических состояний объекта. Завершению процесса диагноза соответствует момент, когда в таблице останется единственный не вычеркнутый столбец. Вычеркивание столбца означает, что объект диагноза неисправен.

Чем меньше число строк таблицы, тем проще процесс диагноза.

Сокращение размерности результатов элементарных проверок дает следующий прием. В каждой строке таблицы все результаты элементарной проверки, 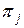, удовлетворяющие условию 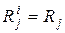, i=1,2,…|S|, принимаются равными 1, остальные результаты этой проверки, для которых имеет место неравенство 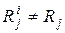, принимаются равными 0, независимо от того, различны они или одинаковы. При этом результат любой элементарной проверки может трактоваться только как положительный 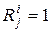или как отрицательный 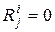. Упрощенную таблицу будем называть двоичной математической моделью объекта диагноза. Заметим, что в этой модели столбец 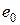, соответствующий исправному состоянию объекта, содержит только положительные результаты элементарных проверок.

Эффективных путей сокращения размеров таблицы нет. Она остается громоздкой и требует больших объемов вычислений. В этом состоит основная причина поиска и разработки различных более экономных способов представления и обработки информации. Платой является отказ от получения точных решений.