Прямые и обратные задачи диагноза

Назовем прямыми задачами диагноза задачи определения по заданной элементарной проверке 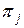той или иной информации о технических состояниях объекта диагноза. При построении алгоритмов диагноза такой информацией может быть, например, определение подмножеств технических состояний объекта, дающих одинаковые результаты элементарной проверки 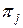. А при реализации алгоритма диагноза интересующей нас информацией может быть определение по известному результату 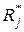элементарной проверки 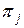подмножества тех технических состояний, в одном из которых фактически находится объект. Указанная информация может представляться не в терминах технических состояний объекта, а в терминах его неисправностей.

Для решения прямых задач диагностирования необходимо предварительно построить математическую модель исправного объекта и произвести необходимое множество допустимых элементарных проверок предполагаемых неисправностей.

В результате решения прямых задач на первом этапе определяется множество тех технических состояний объекта, в одном из которых фактически он находится. Такие задачи решают по результату одной - двух проверок. Далее прогноз уточняют путем использования последующих проверок с применением различных средств и методов контроля. При диагностировании сложных многофункциональных объектов оператору приходится многократно повторять проверки для локализации возникшей неисправности. Часто возникает необходимость в процессе проверок комбинировать различные методы и средства с целью достижения поставленной задачи.

Пусть заданы: математическая модель Ψ исправного объекта диагноза, множество S возможных неисправностей и множество П допустимых элементарных проверок. Модель исправного состояния объекта позволяет ввести в нее любую неисправность 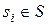и вычислить результаты любой элементарной проверки 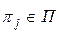по известному значению 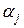ее воздействия.

Вычисление строки таблицы функции неисправностей производится путем многократного решения прямой задачи анализа модели Ψ, состоящего в том, что на модель Ψ подается входное воздействие 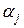элементарной проверки 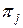и производится вычисление результатов либо 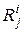, либо 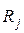. В первом случае в модель предварительно вводится неисправность 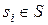(рис.5). В результате будут получены |S|+1 результатов элементарной проверки 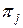для всех i=0,1,2, …, |S|.

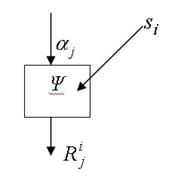
Рис. 5. Представление модели объекта с введением в нее неисправности

Под обратными задачами диагностирования понимается определение некоторой совокупности элементарных проверок, которые позволяют определить заданное техническое состояние объекта, т.е. если в объекте предполагается какая-то неисправность. Решение обратных задач диагностирования позволяет получить все возможные элементарные проверки, обнаруживающие эту неисправность.

Обратные задачи диагностирования заключаются в том, что при известном техническом (неисправном) состоянии изделия необходимо найти такие проверки (методы контроля, программы), которые с высокой степенью точности выявляют это состояние, то есть, возникшую неисправность. Необходимость решения обратных задач диагностирования возникает, как правило, при составлении алгоритмов диагностирования, когда оператору из большого количества методик надо выбрать одну или несколько для практической реализации.

Как и при рассмотрении прямых задач, заданными являются математическая модель исправного объекта, множество возможных неисправностей S и множество П допустимых элементарных проверок. Примем, что модель Ψ позволяет вычислять не только результат 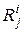, но также для любой неисправности 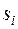вычислять значение 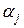воздействия некоторой элементарной проверки 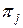по известному ее результату 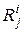, т.е. решать обратную задачу анализа. Построение столбца таблицы функций неисправностей состоит в последовательном вычислении по модели Ψ с введенной в нее неисправностью 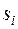результатов 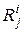каждой элементарной проверки 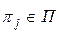. В итоге будут получены |П| результатов 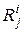элементарных проверок для всех j=1,2, …,|П|. Применение этого алгоритма для каждого i=0,1, …,|S|-1 позволяет заполнить всю П-таблицу функций неисправностей.