Энергия электрического заряда в электрическом поле

При перемещении электрического заряда под действием сил электрического поля происходит изменение его первоначального положения, что влечет за собой изменение потенциальной энергии системы. Поэтому можно утверждать, что работа сил электрического поля совершается за счет изменения (уменьшения) потенциальной энергии:

A = W₁ - W₂ = DW. (1.27)

Формула (1.27) определяет изменение потенциальной энергии, а не её величину. Следовательно, можно условно выбрать такое положение электрического заряда, при котором потенциальная энергия системы равна нулю. Принято считать потенциальную энергию системы зарядов, равной нулю, в том случае, когда один из них удален от другого на бесконечность, т.е., например, W₂ = W = 0. Тогда W₁ = A.

Таким образом, потенциальная энергия заряда, находящегося в электрическом поле другого заряда (потенциальная энергия двух электрических зарядов, системы из двух электрических зарядов), измеряется (численно равна) работой, которую совершают силы электрического поля по удалению одного из зарядов из данной точки поля в бесконечность.

Так как

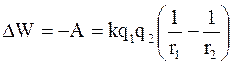(1.28)

и при r₂®¥, W₂®0, в предельном случае при r₂ = ¥, W₂ = 0, то

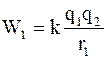. (1.29)

Формула (1.29) определяет потенциальную энергию заряда, находящегося в электрическом поле другого заряда (потенциальную энергию двух электрических зарядов, системы из двух электрических зарядов).

Так как положение зарядов было выбрано произвольно, то в общем случае потенциальная энергия заряда, находящегося в электрическом поле другого заряда (потенциальная энергия двух электрических зарядов, системы из двух электрических зарядов) определяется так:

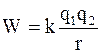, (1.30)

где r – расстояние между центрами взаимодействующих зарядов или до рассматриваемой точки поля, в которую помещается электрический заряд.