Магнитное поле судна. Уравнения пуассона и их анализ.

Корпус судна, его двигатель, судовые механизмы изготовлены из материалов, которые обладают некоторой остаточной намагниченностью. Кроме приобретенной во время постройки остаточной постоянной намагниченности, корпус судна и его механизмы не потеряли способности намагничиваться в магнитном поле Земли, которое постоянно воздействует на судно. Таким образом, в судовом железе можно выделить две составляющие: твердая намагничивается в период постройки и остается постоянной, мягкая составляющая намагничивается в магнитном поле Земли. Постоянный судовой магнетизм и намагничивание мягкого судового железа оказывают влияние на любой магнитный прибор на судне. В этом случае принято говорить, что в пространстве, окружающем судно действует судовое магнитное поле.

Судно со всем его оборудованием является телом весьма сложной формы, поэтому трудно рассчитывать на то, что оно намагничивается однородно. Однако намагничивание судна при постройке и в последующие периоды его плавания происходит в слабом магнитном поле Земли, к тому же магнитная восприимчивость судна, как единого целого невелика. Поэтому неоднородность его намагничивания оказывается незначительной, ею можно пренебречь и исходить из среднего значения намагниченности для всего судна в целом.

Следовательно, можно воспользоваться теоремой Пуассона об однородном намагничивании тел.

Теорема Пуассона формулируется следующим образом: магнитный потенциал U однородно намагниченного тела равен взятому со знаком минус скалярному произведению вектора намагниченности тела 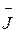на градиент потенциала силы притяжения 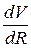, созданного массой данного тела:

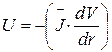
(18)

где r – радиус вектор, совпадающий с направлением наибольшего изменения функции.

Воспользуемся судовыми осями координат

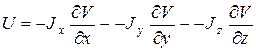
(19)

где: - 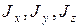- составляющие намагниченности судна по судовым осям

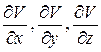- производные величины V по этим осям, пропорциональные потенциалу притяжения, вызванного массой судна.

Чтобы перейти от потенциала к проекциям напряженности магнитного поля на судовые оси, продифференцируем (16) по переменным x, y, z , где J – величина постоянная:

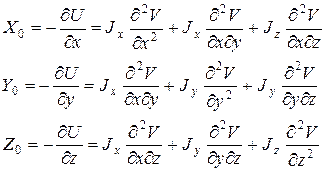
Вектор намагниченности тела выражается формулой (16). Разложим его на составляющие по судовым осям:

,

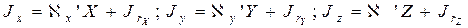где: X, Y, Z - проекции на эти оси намагничивающего поля – магнитного моля Земли.

Подставим эти значения в предыдущие три уравнения:

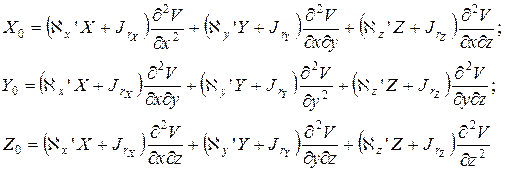
Раскроем скобки в каждом из этих уравнений и введем обозначения

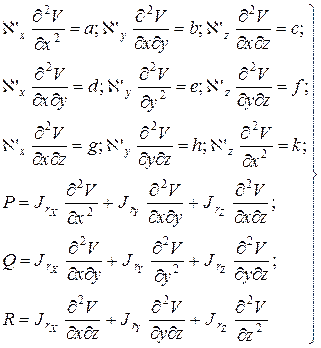
(20)

Пользуясь этими обозначениями, можно записать так:

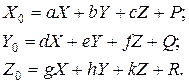
Эти уравнения выражают собой проекции напряженности магнитного поля судна в точке О (см рис). Если в точке О находится компас, то он покажет не только судовой магнетизм, но и воздействие магнитного поля Земли. Сложим алгебраически проекции напряженностей полей судна и Земли, чтобы выразить совместное действие их:

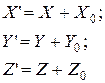
где со штрихом – проекции на судовые оси суммарного магнитного поля, без штриха – проекции на те же оси магнитного поля Земли, с ноликом – проекции напряженности магнитного поля судна. Отсюда:

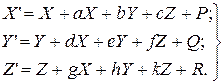
(21)

Эти уравнения получили название уравнений Пуассона, так как они были выведены на основании теоремы Пуассона об однородном намагничивании тел.

a, b, c,…k – параметры Пуассона. Они характеризуют собой мягкое железо: его магнитные качества, форму и размеры, расположение относительно центра компаса.

Слагаемые P, Q, R выражают магнитное поле постоянного судового магнетизма, обусловленного действием жесткого железа.

Все эти величины практически не изменяются для данного компаса и при данном магнитном состоянии судна. Если на судне произвести перемещение больших масс железа относительно компаса или переместить сам компас, то эти величины изменятся.

Курс судна не влияет на эти величины, магнитная широта очень слабо сказывается только на параметры Пуассона. Встряски судна, загрузка судна сказываются на его магнитном состоянии.