Магнитное поле прямолинейного магнита.

До этого мы рассматривали магнит, обладающий магнетизмом одного наименования. Однако любой реальный магнит биполярен, то есть обладает двумя полюсами, в которых сосредоточено равное количество магнетизма двух разных наименований.

Найдем напряженность магнитного поля прямолинейного магнита в виде продолговатого бруска (такая форма принята в компасном деле)

Рассмотрим напряженность магнитного поля в двух точках: находящейся на оси магнита и находящейся на линии перпендикулярной этой оси и проходящей через центр магнита. Магнитные заряды будем считать сосредоточенными в двух крайних точках на концах магнита

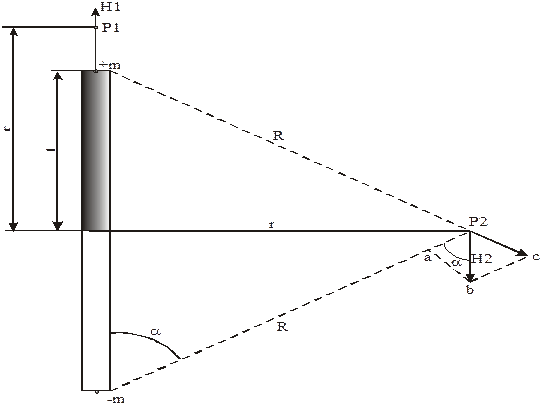
Этот схематический магнит имеет длину 2l, на его концах сосредоточены равные магнитные заряды двух наименований: +m, -m. Найдем напряженность магнитного поля H₁ в точке p₁ находящейся на продолжении оси магнита на расстоянии r от его середины.

Рассмотрим действие ближайшего к точке p₁ полюса магнита с магнитным зарядом +m. В соответствии с выражением (2) это действие в указанной точке выразится напряженностью 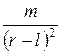. Действие же другого полюса в соответствии с тем же законом будет равно .

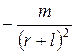Совместное действие полюсов выразится в виде алгебраической суммы этих двух выражений – напряженностей магнитных полей обоих полюсов магнита:

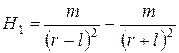
(7)

Алгебраическое суммирование производят потому, что оба полюса и точка, в которой ищут значение поля, лежат на одной прямой, то есть векторы обоих напряженностей составляют одну прямую линию.

Формулой (7) исчерпывается принципиальная сторона вывода. Упростим эту формулу, приведя ее правую часть к общему знаменателю:

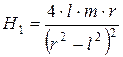
вынесем r² за скобки и, произведя сокращение

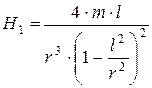
обозначив 2ml=M, получим выражение напряженности магнитного поля схематического магнита в точке, находящейся на продолжении его оси на расстоянии r от центра:

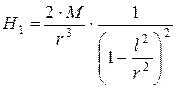
(8)

Буквой M обозначено произведение магнитного заряда m, сосредоточенного на конце магнита, на длину этого магнита 2l. M – по аналогии с механикой –магнитный момент магнита.

Уравнение (8) в применении к схематическому магниту дает точное выражение напряженности. Однако эту формулу можно заменить более удобной для расчетных целей.

Если рассмотреть поле на расстоянии r , значительно большем полудлины магнита l, то дробь 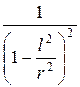можно разложить в биноминальный ряд:

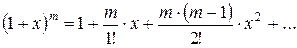
и ограничиться первыми членами разложения

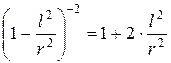
После разложения формула (8) примет такой вид:

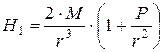
(9)

где: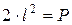

Иногда величина 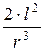бывает настолько мала, что ей можно пренебречь, поэтому

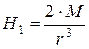
(10)

Решение второй задачи: найдем напряженность H₂ магнитного поля магнита в точке p₂ находящейся на перпендикуляре к оси магнита, восстановленном из его центра. Расстояние от центра магнита до точки p₂ примем равным r.

Отрезок 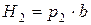является геометрической суммой двух других отрезков 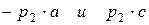, каждый из которых выражает собой напряженность магнитного поля в точке p₂ вызванного магнитными зарядами (-m) и (+m), сосредоточенными в полюсах магнита. Эти напряженности по абсолютному значению равны между собой и каждая из них равняется 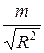, где R – расстояние от точки p₂ до полюсов магнита.

Из подобных треугольников 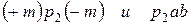можно найти 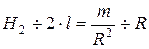отсюда

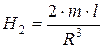
Произведя в этой формуле замену R на 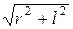и 2ml на M, получим выражение напряженности магнитного поля в точке p₂ , находящейся на перпендикуляре к оси магнита, восстановленном из его середины

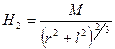
(11)

Формула (11) – точная формула, упростим ее, разложив второй сомножитель в биноминальный ряд

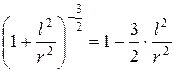
поэтому формула (11) окончательно примет вид:

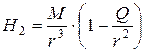
(12)

где: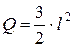

Если принять величину 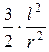бесконечно малой, то

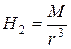
(13)

Выводы

1. Напряженность магнитного поля изменяется обратно пропорционально кубу расстояния. Так, если расстояние до магнита уменьшить вдвое, то напряженность магнитного поля возрастет в 8 раз.

2. Если ось элементарного магнита совместить с направлением на данную точку, а затем повернуть магнит на угол 90° к его первоначальному направлению, оставляя расстояние r неизменным, то напряженность магнитного поля уменьшится вдвое.