Передаточная функция многомерной САУ

Многомерные объекты содержат по две, три, и более выходных величин. Число уравнений для статической модели или динамической модели должно соответствовать числу выходных величин. Наиболее простыми из многомерных объектов являются двухмерные объекты. Их выходные величины могут влиять или не влиять одна на другую. Примером двухмерного объекта может служить резервуар для жидкости.

В многомерных объектах с независимыми выходными величинами изменение любой из входных величин приводит к изменению только своей выходной величины. Такие объекты можно разбить на несколько одномерных объектов и рассматривать их независимо один от другого.

В многомерных объектах с взаимозависимыми выходными величинами изменение входных величин приводит к одновременному изменению нескольких выходных величин, что объясняется наличием в таких объектах каналов перекрестных связей. Примером двухмерного объекта с перекрестными связями является экзотермический реактор идеального перемешивания.

Многомерная система, содержащая произвольное число выходных величин m и входных воздействий n описывается передаточными функциями

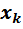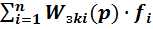= , k=1, 2, 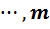(17)

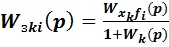Здесь (18)

- передаточная функция замкнутой системы, определяющая зависимость k-ой выходной величины 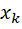от i - ого входного воздействия.

Систему уравнений 17 удобно представить матрично-векторным уравнением:

x= 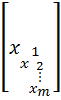- вектор-столбец

f= 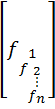- вектор-столбец

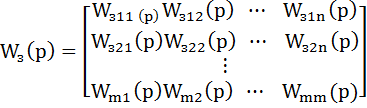(19)

- матрица размера m 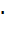n.