Квантовый гармонический осциллятор

Осциллятором называют физическую систему, совершающую колебания. Если колебания описываются синусоидальной функцией, то такой осциллятор называется гармоническим. Примерами классических осцилляторов могут служить математический маятник, груз на пружине и т.д. Движение этих осцилляторов происходит под действием квазиупругой силы , где x - отклонение осциллятора от положения равновесия, k - упругая постоянная. Потенциальная энергия гармонического осциллятора

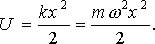(1.36)

Понятие осциллятора применяется также к немеханическим колебательным системам. В частности, электрический колебательный контур является электрическим осциллятором.

В квантовой механике понятие силы не используется. Поэтому аналогом классического осциллятора в квантовой физике будет квантовый гармонический осциллятор, состояние которого описывается уравнением Шредингера с потенциальной функцией вида (1.36). Такие квантовые колебания совершают атомы в молекулах, ионы в узлах кристаллической решетки твердого тела (фононы), валентные электроны в твердых телах относительно ионного остова (плазмоны) и др.

Стационарное уравнение Шредингера для одномерного случая (линейный гармонический осциллятор) имеет вид

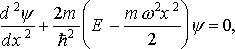(1.37)

здесь, как обычно в квантовой механике, Е - полная энергия квантового осциллятора.

Уравнение (1.37) имеет решения только при значениях энергии Еn, равных

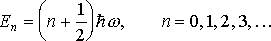(1.38)

Энергетические уровни квантового гармонического осциллятора эквидистантны, т.е. находятся на равных расстояниях друг от друга (рис. 1.5). На этом рисунке через ±x_0n обозначены точки поворота классического осциллятора с такой же энергией E_n, как и у квантового осциллятора.

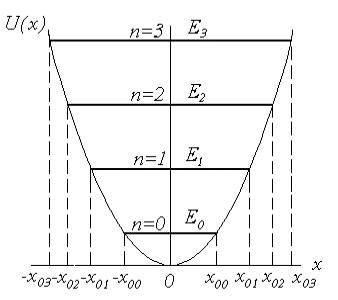
Рис. 1.5. Схема энергетических уровней квантового гармонического осциллятора

Таким образом, полная энергия квантового гармонического осциллятора может принимать только определенные дискретные значения. Наименьшее возможное значение энергии 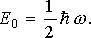Существование отличного от нуля минимального значения энергии квантового гармонического осциллятора, так же как и для частицы в потенциальной яме, с неизбежностью вытекает из принципа неопределенностей Гейзенберга. Можно показать, что - 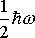это как раз та минимальная энергия, которой должен обладать квантовый гармонический осциллятор, чтобы соотношения неопределённостей были удовлетворены.

Собственные волновые функции квантового гармонического осциллятора могут быть представлены в виде 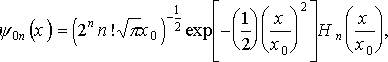(1.39)

где - 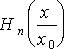полиномы Чебышева-Эрмита.

Полиномы Чебышева-Эрмита низших степеней имеют вид

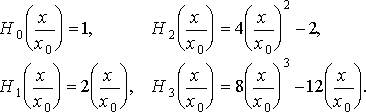
Из свойств полиномов Чебышева-Эрмита следует, что все их корни некратные и вещественные. Число корней полинома равно его степени n, в чем легко убедиться, анализируя приведенные выше выражения для полиномов низших степеней. На рис. 1.6 приведены распределения плотности вероятности 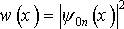для основного состояния квантового гармонического осциллятора (n = 0) и для двух возбужденных состояний (n = 1 и 5). На этом же рисунке показаны штриховыми кривыми вероятности найти частицу в окрестности точки x для классического осциллятора, совершающего гармонические колебания с теми же значениями полной энергии Е. Вертикальные штриховые линии соответствуют точкам поворота классического осциллятора ± x₀₀, ± x₀₁, ± x₀₅, и т.д. Эта вероятность, очевидно, пропорциональна его скорости, т.е. обратной величине квадратного корня из кинетической энергии. Следовательно, для классического осциллятора 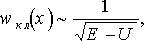, где Е и U - полная и потенциальная энергия соответственно. Отсюда видно, что вблизи точек поворота w_кл(x) стремится к бесконечности. Вблизи положения равновесия скорость осциллятора максимальна и соответственно классическая вероятность минимальна.

При малых n, что соответствует низшим энергетическим состояниям, квантовый и классический осцилляторы существенно ведут себя по разному. Однако при достаточно больших энергиях функция 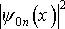приближается к классической функции распределения как к некоторой средней величине, относительно которой она совершает быстрые осцилляции.

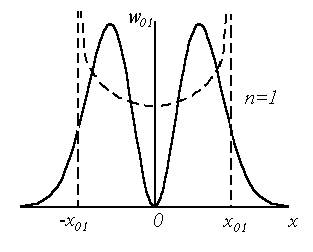
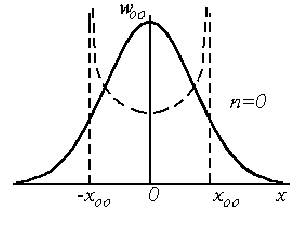
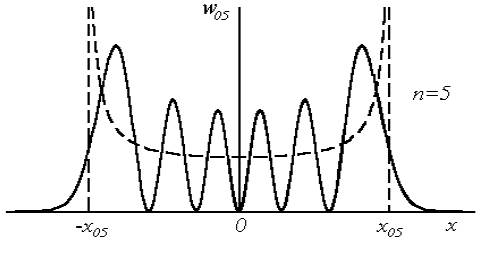
Рис.1.6. Распределение плотности вероятности для трех состояний квантового гармонического осциллятора

Отметим еще одну особенность квантово-механического осциллятора. Как видно из рис. 1.6, вероятность обнаружить микрочастицу, совершающую квантово-механические колебания вне пределов, ограничивающих движение классического осциллятора, не равна нулю! Такое поведение квантово-механического осциллятора связано с более общим свойством микрочастиц проникать за пределы потенциальных барьеров, недоступных с точки зрения классической физики. Эта проблема будет подробно рассмотрена в следующем разделе.