Символический (комплексный) метод расчета

Расчет синусоидальных токов с применением комплексных чисел получил название символического (комплексного) метода. Он является основным методом расчета установившихся режимов в цепях переменного синусоидального тока.

Последовательность расчета синусоидальных токов символическим методом.

1. Ввести комплексные токи, сопоставить синусоидальным ЭДС комплексные ЭДС, определить комплексные сопротивления ветвей.

2. Составить систему уравнений Кирхгофа для комплексных токов.

3. Решив эту систему, определить комплексные токи.

4. По найденным комплексным токам найти синусоидальные токи.

Система уравнений Кирхгофа в комплексной форме и система уравнений Кирхгофа для цепи постоянного тока относятся к одному классу уравнений (это линейные алгебраические уравнения). Различие состоит только в том, что в первой системе коэффициенты являются комплексными, а во второй - действительными числами. Поэтому расчет цепей переменного синусоидального тока символическим методом в общем виде (то есть в алгебраических выражениях, без вычислений) мало чем отличается от расчета цепей постоянного тока. В этом заключается главное достоинство символического метода.

Комплексное сопротивление ветви

Рассмотрим электрическую цепь, состоящую из одной ветви, в которой резистор, катушка и конденсатор соединены последовательно . Действующее значение приложенного синусоидального напряжения равно U , а круговая частота ω. Параметры цепи R,L и C считаются известными, требуется определить действующее значение тока I.

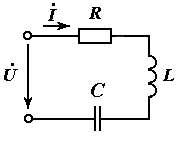
По второму закону Кирхгофа

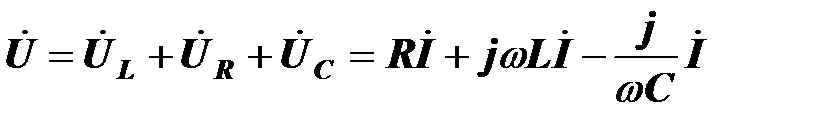
Комплексный ток

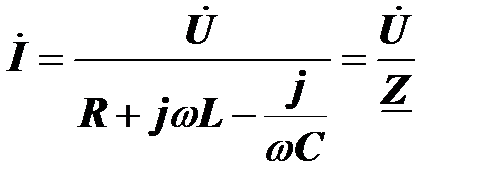
В последнем выражении комплексный параметр

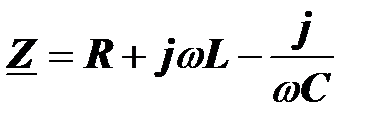
называется комплексным сопротивлением (в рассматриваемом примере - это комплексное сопротивление ветви).

Комплексное сопротивление ветви равно сумме комплексных сопротивлений содержащихся в ней элементов

В данном примере

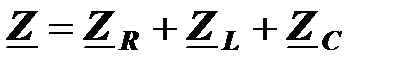
Действующее значение тока равно модулю комплексного тока

,

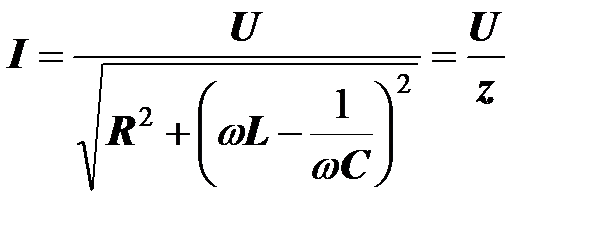где

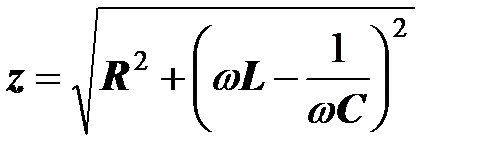
-полное сопротивление ветви.

Формулу

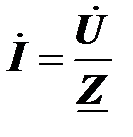
часто называют законом Ома в комплексной форме по аналогии с формулой

.

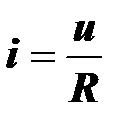Комплексное сопротивление двухполюсника

Комплексный ток на входе любого линейного пассивного двухполюсника пропорционален приложенному к нему комплексному напряжению.

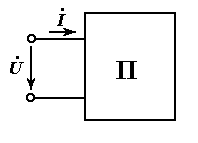
Коэффициент пропорциональности между приложенным комплексным напряжением и входным комплексным током называется комплексным сопротивлением пассивного двухполюсника

.

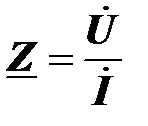Модуль комплексного сопротивления равен полному сопротивлению двухполюсника, аргумент комплексного сопротивления равен углу сдвига фаз между напряжением и током:

.

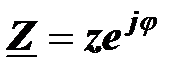Доказательство,

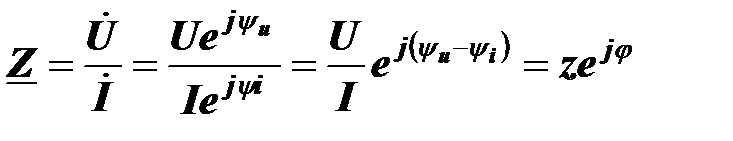
где

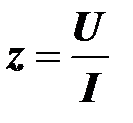
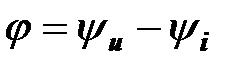
Действительная часть комплексного сопротивления равна эквивалентному активному сопротивления двухполюсника, мнимая часть комплексного сопротивления – эквивалентному реактивному сопротивлению

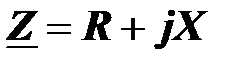
Доказательство

,

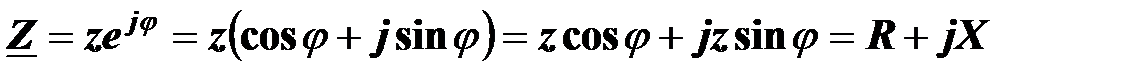Комплексная проводимость двухполюсника

Комплексная проводимость двухполюсника – это величина, обратная его комплексному сопротивлению,

.

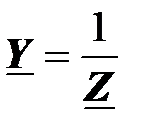Комплексная проводимость играет роль коэффициента пропорциональности между входным комплексным током и комплексным напряжением, приложенным к двухполюснику,

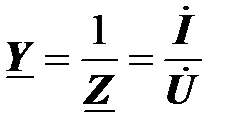
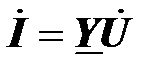
Модуль комплексной проводимости равен полной проводимости двухполюсника, аргумент комплексной проводимости равен сдвигу фаз между напряжением и током с обратным знаком:

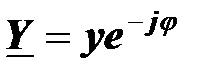
Доказательство

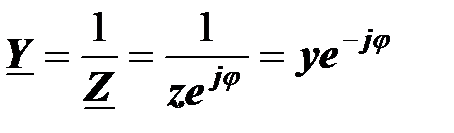
где использовано определение полной проводимости

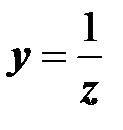
Действительная часть комплексной проводимости равна эквивалентной активной проводимости двухполюсника, а мнимая часть равна эквивалентной реактивной проводимости двухполюсника с обратным знаком:

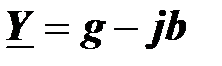
Доказательство

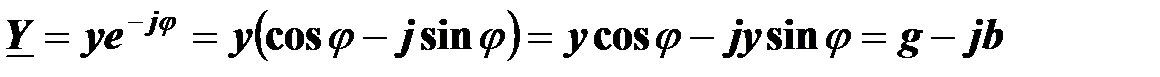
где использованы свойства эквивалентной активной проводимости

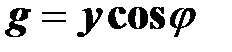
и эквивалентной реактивной проводимости двухполюсника

.

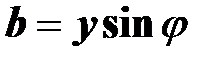Зависимость между эквивалентным сопротивлением и эквивалентной проводимостью двухполюсника

Как уже отмечалось, комплексное сопротивление и комплексная проводимость – это обратные величины

, .

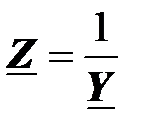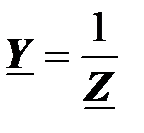Рассмотрим подробнее первую из этих формул:

.

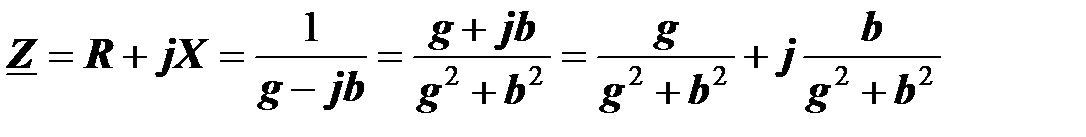Приравнивая по отдельности действительные и мнимые части второго и последнего выражений в этой цепочке выражений, получаем зависимости эквивалентных сопротивлений (активного и реактивного) от эквивалентных проводимостей двухполюсника (активной и реактивной):

, .

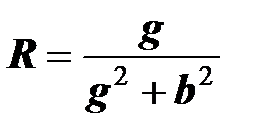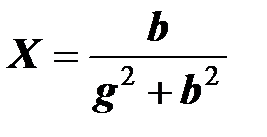Вторая из двух исходных формул после аналогичных преобразований дает выражения эквивалентных проводимостей через эквивалентные сопротивления двухполюсника:

, .

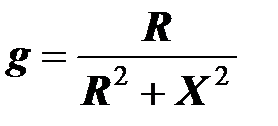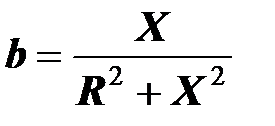Экспериментальное определение параметров двухполюсника с помощью амперметра, вольтметра и ваттметра

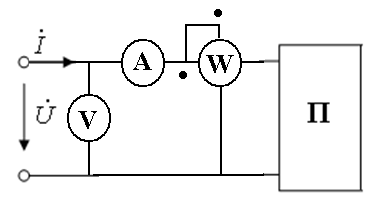
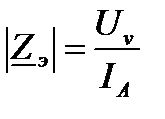
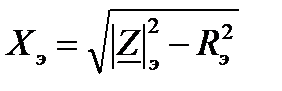
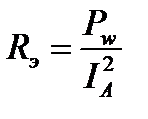
Экспериментальное определение знака реактивного сопротивления с помощью амперметра и емкости С’

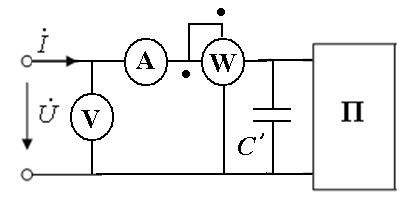
уменьшение показания амперметра после подключения емкости С’ говорит о положительном знаке реактивного сопротивления двухполюсника