ПРИБЛИЖЕНИЕ НУЛЕВОГО ДИФФЕРЕНЦИАЛЬНОГО ПЕРЕКРЫВАНИЯ И ОРТОГОНАЛИЗОВАННЫЕ АО

Число интегралов кулоновского отталкивания электронов можно резко сократить, используя приближение нулевого дифференциального перекрывания (НДП), введенное впервые Парром в 1952г. Это приближение, сыгравшее важную роль в становлении и развитии полуэмпирических методов, основано на том, что многие интегралы кулоновского отталкивания электронов близки к нулю, особенно те, которые включают в себя функции типа c_m(1)c_n(1) с m¹n. Интегралы, содержащие произведения c_m(1)c_m(1) как правило, существенно больше по величине. Поэтому предлагается упрощение типа

(mn|ls) = (mm|ll)d_mnd_ls (1)

т. е. предполагается, что орбитали c_m и c_n практически не перекрываются в пространстве и

c_mc_ndt = 0 (2)

Интегралы перекрывания АО, входящие в уравнения Рутаана и участвующие в нормировке молекулярных орбиталей, также полагаются равными нулю для m¹n:

S_mn = òc_m (1)c_n (1)dt = d_mn (3)

Несколько нарушают стройность и логическую последовательность приближения НДП остовные интегралы Н_mnкоторые должны быть равны нулю, если справедливо (2). Оказывается, однако, что если положить их равными нулю и сохранить последовательность приближения (2), то результаты расчетов весьма неудовлетворительны. В связи с этим интегралы Н_mn считаются отличными от нуля и рассматриваются как варьируемые параметры, определяющие параметризацию.

Приближение (1) превращает четырехмерный массив интегралов (mn|ls) в двумерный. Вместе с сокращением числа подлежащих расчету интегралов уменьшается также и время вычисления одного интеграла, так как двухцентровые интегралы считаются намного проще трех- и четырехцентровых. Для N=10 (число базисных функций) необходимо вычислить только 45 двухцентровых .интегралов, в то время как общее число интегралов (mn|ls) равно при этом базисе 4595.

Приближение (2) справедливо достаточно точно в базисе ортогональных атомных орбиталей. Переход от неортогонального базиса c_i (i=l, 2, ... , N) кортогональному можно осуществить преобразованием Левдина

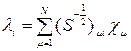, (4)

где:

S_mi = òc_m (1)c_i (1)dt (5)

Матрица S^-1/2 определяется из условия

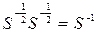(6)

Если приближение НДП используется для всех пар атомных орбиталей, то уравнения Рутаана примут вид

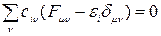(7)

где элементы матрицы Фока записываются следующим образом:

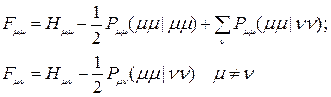(8)

Мы отмечали выше, что приближения, вводимые в метод Рутаана, не должны отражаться на инвариантности полной волновой функции к ортогональным преобразованиям базиса атомных орбиталей. Рассмотрим влияние приближения НДП на инвариантность полуэмпирических методов к ортогональным преобразованиям базиса.

ИНВАРИАНТНОСТЬ ПОЛУЭМПИРИЧЕСКИХ МЕТОДОВ

Уравнения Рутаана инвариантны к ортогональным преобразованиям молекулярных орбиталей. Если мы имеем молекулярные орбитали,

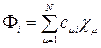(9)

то ортогональным преобразованием можно перейти к другим базисным функциям

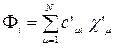(10)

Причем 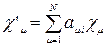(11)

где а_mn - несингулярная квадратная матрица (ее определитель не равен нулю.)

Вычисления методом Рутаана с функциями (9) и (10) должны приводить к одинаковым орбитальным энергиям и соответственно к одинаковой полной энергии. Вместе с тем коэффициенты разложения МО в ЛКАО c_mi и c'_miбудут отличаться.

Рассмотрим, какие преобразования могут описываться

соотношением (11).

1. Преобразование, смешивающее орбитали одного атома с одинаковыми nи l и приводящее к их линейной комбинации. Например, можно смешать 2р_х- 2р_у-, 2p_z-AOили пять 3d-функций. Наиболее важным примером такого преобразования служит поворот декартовой системы координат, выбранной для определения атомных орбиталей.

2. Преобразования, которые позволяют смешивать любые атомныеорбитали одного атома. Если смешиваются функции с разными l, то получаются гибридные АО. Например, если смешаем 2s-, 2p_x-, 2р_у-, 2p_z-AO, то получим sр³-гибридные АО. В этом случае c_m’ — гибридные базисные функции.

3. Преобразования, позволяющие смешивать функции разных атомных центров. Эти трансформации ведут к неатомному базису. Примером такого преобразования может служить переход к локализованным МО.

Уравнения Рутаана, а следовательно, матричные элементы F_mnинвариантны к рассмотренным преобразованиям. Введение приближения (2) нарушает инвариантность уравнений. Рассмотрим условия, которые необходимо наложить на интегралы (mm/nn), H_mnи H_mm, с тем, чтобы восстановить инвариантность. Мы займемся только преобразованиями типа 1 и 2, преобразования последнего вида рассматриваться не будут.

Дифференциальное перекрывание c_mc_n может быть двухатомным и одноатомным в зависимости от того, принадлежат орбитали c_mи c_n одному или разным атомам. Очевидно, что преобразования типа 1 и 2 переводят двухатомное дифференциальное перекрывание c_mc_n в другое перекрывание c_m’c_n’. Если мы пренебрегаем двухатомным дифференциальным перекрыванием для всех пар атомов, т. е. c_mc_ndt = 0, то отсюда следует, что и c’_mc’_ndt = 0

Другими словами, пренебрежение двухатомным дифференциальным перекрыванием сохраняет инвариантность к преобразованиям типа 1 и 2. Метод, в котором пренебрегают только двухатомным дифференциальным перекрыванием, называется методом NDDO (ПДДП – пренебрежение двухатомным дифференциальным перекрыванием). Этот метод достаточно сложен и по затратам машинного времени мало отличается от неэмпирических методов. Поэтому он не получил пока широкого распространения.

Случай дифференциального перекрывания орбиталей, принадлежащих одному атому, более сложен. Рассмотрим двухцентровый интеграл (p_xp_y|s²), где р_х и р_у — орбитали одного атома. В приближении НДП этот интеграл обращается в нуль. Повернем декартову систему координат на угол q относительно оси z.Тогда можем записать

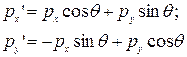(12)

В новой системе координат интеграл (p_x’p_y’|s²) отличен от нуля. Действительно,

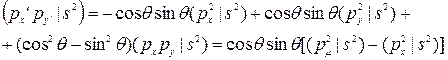(13)

При получении окончательного вида мы учли, что функции р_х и р_уортогональны. Из (13) видно, что равенство обращается в нуль только-при q = 0,90°, т. е. оно несправедливо при любом q. Итак, интегралы кулоновского отталкивания не инвариантны относительно преобразований системы координат в том случае, если они включают в себя перекрывание двух АО одного атома. Аналогично можно показать, что они неинвариантны к гибридизационным изменениям.

Выход из создавшейся ситуации был предложен в 1965 г. Поплом с сотрудниками, которые разработали метод CNDO (ППДП – полное пренебрежение дифференциальным перекрыванием). Этот метод в настоящее время является наиболее разработанным полуэмпирическим методом, включающим как s- так и p-электроны.

МЕТОД CNDO

В методе CNDO учитываются только валентные электроны атомов, внутренние электроны включаются в неполяризованный остов. Приближение НДП принимается для всех пар атомных орбиталей, в том числе и для принадлежащих одному атому. Для восстановления нарушаемой при этом инвариантности необходимо предположить, что

(p_y²|s²) = (p_x²|s²) (14)

В трехмерном случае имеем

(p_y²|s²) = (p_x²|s²) = (p_z²|s²) = (p²|s²) (15)

Это соответствует предположению, что р-функция имеет сферическую симметрию, аналогичную s-орбитали. Интеграл (p²|s²) должен быть равен интегралу (s’²|s²), где s' — сферическая орбиталь, имеющая ту же радиальную часть, что и р-АО.

Рассмотрение преобразований второго типа приводит к требованию

(s’²|s²) = (s²|s²) (16)

Таким образом, для сохранения инвариантности при введении при­ближения НДП необходимо выполнение условия

(mm|nn) º g_mn = g_AB, mÎA, nÎB (17)

Истинное отталкивание между орбиталями заменяется средним отталкиванием между электронами атомов А и В, g_AB вычисляются с s-функциями соответствующих атомов:

g_AB = (s_A²|s_B²) (18)

Инвариантность метода достигается за счет отказа от индивидуальности орбиталей и сведения электронного распределения атомов к сферически симметричному. Различие орбиталей будет проявляться в интегралах перекрывания и величинах U_mm (U_mm - характеристикаорбитали m атома А и представляет собой энергию электрона, находящегося на орбитали m свободного атома А. Ее значение обычно получают полуэмпирически, используя результаты спектральных исследований атомов.)

МЕТОД INDO

Метод INDO (ЧПДП – частичное пренебрежение дифференциальным перекрыванием) занимает промежуточное по сложности и времени вычислений положение между методами NDDO и CNDO.

Недостатком метода CNDO является пренебрежение отличием в кулоновском отталкивании электронов с параллельными и антипараллельными спинами. Это отличие особенно велико для электронов одного атома, в этом случае двухэлектронный обменный интеграл (mn|mn)m, nÎA представляет собой разницу в энергии взаимодействия электронов в синглетном и триплетном состояниях. В методе CNDO эти интегралы полагаются равными нулю, вследствие чего этот метод не может даже качественно воспроизвести правило Гунда, согласно которому два электрона на различных орбиталях одного атома отталкиваются слабее в случае параллельности их спинов. Метод CNDO плохо работает в случае триплетных состояний, свободных радикалов, т. е. для молекулярных систем с достаточно большой обменной энергией.

В методе INDO в значительной мере устраняются эти недостатки путем сохранения только одноцентровых обменных интегралов (mn|mn).

Метод INDO имеет преимущества перед CNDO только при расчете электронной структуры молекул с открытыми оболочками (S¹0). Для закрытых оболочек результаты расчетов методом CNDO более предпочтительны и требуют меньших затрат машинного времени.

Дьюар модифицировал метод INDO применительно к расчету свойств основных состояний молекул, введя эмпирическую оценку некоторых кулоновских, а также остовных интегралов с тем, чтобы получить правильные значения теплот образования молекул. Этот метод получил название MINDO (МЧПДП – модификация частичного пренебрежения дифференциальным перекрыванием).