Организация процесса оптимизации в динамическом программировании

Выше было отмечено, что при выборе шагового управления необходимо учитывать следующие требования:

1. возможные исходы предыдущего шага ;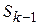

2. влияние управления 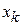на все оставшиеся до конца процесса шаги.

В задачах динамического программирования первое требование учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение второго требования обеспечивается тем, что в этих задачах условная оптимизация проводится от конца процесса к началу.

Условная оптимизация.На первом этапе решения задачи, называемом условной оптимизацией, определяются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего в соответствии с алгоритмом обратной прогонки. На последнем, n-м шаге оптимальное управление - 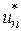определяется функцией Беллмана: 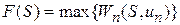, в соответствии с которой максимум выбирается из всех возможных значений 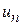, причем .
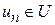Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге. В общем виде это уравнение имеет вид

, .

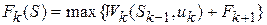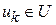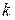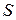Этот максимум (или минимум) определяется по всем, возможным для и , значениям переменной управления .

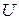Безусловная оптимизация.После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый, осуществляется второй этап решения задачи, называемый безусловной оптимизацией. Пользуясь тем, что на первом шаге ( 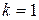) состояние системы известно - это ее начальное состояние 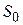, можно найти оптимальный результат за все шагов и оптимальное управление на первом шаге 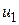, которое этот результат доставляет. После применения этого управления система перейдет в другое состояние 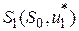, зная которое, можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге 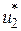, и так далее до последнего -го шага. Вычислительную схему динамического программирования можно строить на сетевых моделях (как в случае с черепашкой), а также по алгоритмам прямой прогонки (от начала) и обратной прогонки (от конца к началу).

Список литературы

1. Калиткин Н.Н. Численные методы. – М.: “Наука”, 1991.

2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатом издат, 1987.

3. Мину М. Математическое программирование. Теория и алгоритмы: Пер. с фр. И предисловие Штерна. – М.: Наука. Гл. ред. физ-мат.лит., 1990.– 488 с.

4. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М., Методы оптимизации. М.: – Наука, 1978.

5. Работы выпускные квалификационные, проекты и работы курсовые. Структура и правила оформления. СТО ТПУ 2.5.01-2006

6. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике: В 2-х кн. Кн.1. Пер. с англ.- М.: Мир, 1986.

7. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986.