Постановка задачи динамического программирования
В технике существует обширный класс объектов и процессов, управление которыми осуществляется на основе ограниченного числа решений, принимаемых последовательно в некоторые фиксированные моменты времени. Определение закона управления для таких процессов связано с решением, так называемой задачи многокритериального выбора. В отличие от обычной вариационной задачи, когда управление ищется в форме некоторой функциональной зависимости (от времени или координат), сразу переводящей объект из одного состояния в другое, здесь рассматриваются процессы управления, состоящие из ряда шагов. При этом управляющие воздействия генерируются на каждом шаге и в течение этого шага остаются неизменными.
Подобные законы управления характерны для объектов дискретных по своей физической природе. Например, путешествие черепашки четко распадается на ряд этапов, в начале каждого из которых необходимо принять решение, в какую сторону двигаться.
К подобной схеме может быть сведен и процесс управления непрерывным объектом, если он управляется дискретным регулятором.
Рассмотрим задачу общего вида, характерную для метода динамического программирования. Пусть это будет задача о распределении ресурсов между предприятиями. В результате управления инвестициями система последовательно переводится из начального состояния 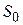 в конечное
в конечное 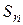 . Предположим, что управление можно разбить на
. Предположим, что управление можно разбить на  шагов и решение принимается последовательно на каждом шаге, а управление представляет собой совокупность
шагов и решение принимается последовательно на каждом шаге, а управление представляет собой совокупность  пошаговых управлений. На каждом шаге необходимо определить два типа переменных - переменную управления
пошаговых управлений. На каждом шаге необходимо определить два типа переменных - переменную управления 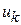 и новую переменную состояния системы
и новую переменную состояния системы 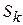 . (Если сравнивать с Черепашкой, то это время в пути и дальнейшее направление движения из каждой клетки). Переменная
. (Если сравнивать с Черепашкой, то это время в пути и дальнейшее направление движения из каждой клетки). Переменная 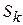 определяет, в каких состояниях может оказаться система на рассматриваемом
определяет, в каких состояниях может оказаться система на рассматриваемом 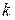 -м шаге. При этом предполагается,
-м шаге. При этом предполагается, 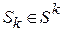 , где
, где 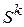 некоторое множество состояний, в которые объект может оказаться в результате всех
некоторое множество состояний, в которые объект может оказаться в результате всех 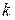 предыдущих шагов. В зависимости от состояния
предыдущих шагов. В зависимости от состояния 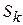 на этом шаге следует применить некоторые управления, которые характеризуются переменной
на этом шаге следует применить некоторые управления, которые характеризуются переменной 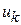 . Все переменные управления удовлетворяют определенным ограничениям, т.е. являются допустимыми. Пусть
. Все переменные управления удовлетворяют определенным ограничениям, т.е. являются допустимыми. Пусть 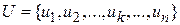 - управление, переводящее систему из состояния
- управление, переводящее систему из состояния 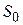 в состояние
в состояние 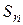 , a
, a 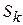 - состояние системы на k-м шаге управления. Тогда последовательность состояний системы можно представить в виде графа, представленного на рис. 6.2.
- состояние системы на k-м шаге управления. Тогда последовательность состояний системы можно представить в виде графа, представленного на рис. 6.2.
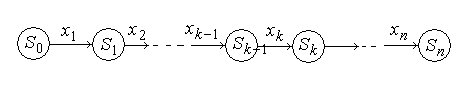
Рис. 6.2.
Применение управляющего воздействия 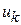 на каждом шаге переводит систему в новое состояние
на каждом шаге переводит систему в новое состояние 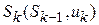 и приносит некоторый результат
и приносит некоторый результат 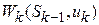 .
.
Функционал, оптимизацию которого необходимо обеспечить путем выбора оптимального управления, выражается суммой
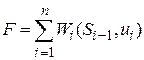 .
.
Сформулированную задачу можно интерпретировать как отыскание экстремума сложной функции большого числа (в данном случае  ) переменных
) переменных 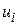 . При значительном числе переменных эта задача представляет очень большие сложности. Вместо этого в методе ДП рассматривается многошаговый процесс принятия решений на основе так называемого принципа оптимальности, впервые сформулированного в 1953 г. Р.Э.Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая выигрыш на данном шаге.
. При значительном числе переменных эта задача представляет очень большие сложности. Вместо этого в методе ДП рассматривается многошаговый процесс принятия решений на основе так называемого принципа оптимальности, впервые сформулированного в 1953 г. Р.Э.Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая выигрыш на данном шаге.
Следуя принципу оптимальности для каждого возможного состояния на каждом шаге среди всех возможных управлений выбирается оптимальное управление 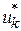 , такое, чтобы результат, который достигается за шаги с k-го по последний n-й, оказался бы оптимальным.
, такое, чтобы результат, который достигается за шаги с k-го по последний n-й, оказался бы оптимальным.
Пример. Пусть Вам необходимо пробежать 3 километра. Пусть 1 километр Вы уже пробежали и нужно принять решение как бежать дальше. Если вы хотите показать максимальный результат, Вы должны принять решение, которое будет оптимальным на данный момент, исходя из Вашего состояния и оставшейся части дистанции. Вы не можете резко ускориться в угоду сиюминутному результату. Вы должны бежать так, чтобы показать наилучший результат на всей дистанции.
Здесь нужно отметить два фактора.
1. Ваша дальнейшая стратегия бега зависит только от того, как вы чувствуете себя на данный момент.
2. Начальный участок дистанции не являлся оптимальным с точки зрения преодоления 1 километра. Т.е. оптимальная траектория не есть сумма оптимальных участков. Оптимальным является только последний участок траектории.
Числовая характеристика этого результата 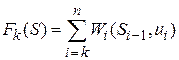 называется функцией Беллмана и зависит от номера шага
называется функцией Беллмана и зависит от номера шага 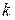 и состояния системы
и состояния системы 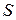 . Задача динамического программирования формулируется следующим образом:
. Задача динамического программирования формулируется следующим образом:
требуется определить такое управление 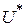 , переводящее систему из начального состояния
, переводящее систему из начального состояния 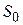 в конечное состояние
в конечное состояние 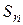 , при котором целевая функция принимает наибольшее (наименьшее) значение
, при котором целевая функция принимает наибольшее (наименьшее) значение 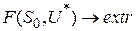 .
.
Дата добавления: 2020-03-17; просмотров: 772;











