Динамическое программирование

Динамическое программирование — это вычислительный метод для решения задач определенной структуры. Возникло и сформировалось в 1950-1953 гг. благодаря работам Р. Беллмана над динамическими задачами управления запасами. В упрощенной формулировке динамическое программирование представляет собой направленный последовательный перебор вариантов, который обязательно приводит к глобальному максимуму.

Применим следующий вариант знакомства с методом динамического программирования. Сначала решим конкретную простую задачу, а потом обобщим метод на весь круг задач, решаемых этим методом.

Задача о Черепашке

Постановку задачи динамического программирования рассмотрим на примере классической задачи о Черепашке. Черепашке необходимо попасть из пункта 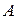в пункт 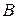. На каждом углу она может поворачивать только вверх или только вправо. Время движения по каждому отрезку пути указано на рисунке 6.1. Требуется найти минимальное время, за которое Черепашка может попасть из пункта 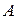в пункт .

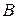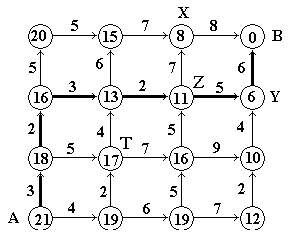
Рис. 6.1 Задача о Черепашке

Путь, показанный на рисунке жирными линиями со стрелкой, требует 21 единицу времени. Отметим, что каждый путь состоит из 6 шагов: трех вверх и трех вправо. Количество возможных путей Черепашки – 20. Мы можем перебрать все пути и выбрать самый быстрый. Это метод полного перебора (ответ - 21). Для вычисления каждого времени требуется пять операций сложения, а для нахождения ответа 100 операций сложения и 19 операций сравнения. Задача решается вручную. Однако при N равном 8, у Черепашки уже 12870 путей. Подсчет времени для каждого пути требует 15 операций сложения, а в целом - 193050 сложений и 12869 сравнений, то есть порядка 200000 операций. Компьютер при быстродействии 1000000 операций в секунду найдет решение за 0.2 секунды, а человек? Предположим, что N равно 30, тогда количество различных путей 60!*(30!*30!). Это очень большое число, его порядок 10¹⁷. Количество операций, необходимых для поиска решения, равно 60*10¹⁷. Компьютер с быстродействием 1000000 операций в секунду выполнит за год порядка 3.2*10¹³ операций. Не трудно прикинуть количество лет, требуемых для решения задачи.

Вернемся к исходной задаче. Начнем строить путь Черепашки от пункта 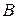. Каждому углу присвоим вес, равный минимальному времени движения Черепашки от этого угла до пункта 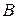. Как его находить? От углов 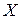, 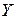очевидно. Для угла 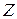время движения Черепашки в пункт 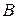через угол 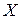15 единиц, а через угол 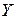11 единиц. Берем минимальное значение, то есть вес угла будет равен 11. Продолжим вычисления. Их результаты приведены на рисунке. Путь, отмеченный стрелками, является ответом задачи. Оценим количество вычислений. Для каждого угла необходимо выполнить не более двух операций сложения и одной операции сравнения, то есть три операции. При N, равном 300, количество операций - 3*301*301, это меньше 1000000, и компьютеру потребуется меньше одной секунды. Итак, много лет при N=30 и 1 секунда при N=300.

Выделим особенность задачи, которая позволяет решить ее описанным способом. Мы начинаем с угла 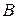, и для каждого угла найденное число является решением задачи меньшей размерности. Поясним эту мысль. Если бы мы решали задачу поиска пути Черепашки из пункта 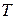в пункт 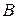, то найденное число 17 - решение задачи. Для каждого угла найденное значение времени не изменяется и может быть использовано на следующих этапах.