Гидродинамическое подобие

ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕХАНИКИ ПЕЧНЫХ ГАЗОВ

В практической деятельности каждого инженера-металлурга приходится решать задачи, связанные с движением газов: определять их количество, измерять давления, потери давления.

Применение теории подобия

В промышленности часто встречаются агрегаты, непосредственное исследование которых затруднено или вообще невозможно. К таким агрегатам относятся и металлургические печи, работающие при высокой температуре рабочего пространства. В некоторых случаях единственно возможным методом исследования процессов, протекающих в рабочем пространстве, является метод исследования на модели печи. При этом процессы в модели должны быть подобны процессам, протекающим в печи. Для достижения этого необходимо, чтобы при создании модели и проведении опытов на ней были выдержаны условия, определяемые теорией подобия.

Необходимые условия подобия двух физических явлений:

- Должны быть тождественны (одинаковы) безразмерные математические уравнения, описывающие два явления. Это возможно, если явления одной физической природы. Например, подобие между движением газа в газоходах разного размера. Однако этого еще недостаточно для обеспечения подобия двух физических явлений. Необходимо еще соблюдение и других условий.

- Необходимо подобие условий однозначности. Условиями однозначности являются такие условия, которые из массы явлений, природа которых аналогична, выделяют какое-то конкретное явление. Например, геометрическое подобие двух рассматриваемых явлений. Но и этого еще недостаточно.

- Рассматриваемое ниже уравнение Бернулли для течения реальной жидкости справедливо для огромного множества видов течения различных жидкостей. Чтобы из этого множества течений выделить два подобных, необходимо (кроме геометрического подобия) подобие вязкостно-скоростных характеристик.

При этом масштабные преобразования применяются и к физическим явлениям, уравнения которых в отличие от геометрических уравнений включают величины, имеющие различную размерность. Поэтому при рассмотрении подобия физических явлений следует сравнивать величины с одинаковой равномерностью.

Гидродинамическое подобие

Для металлургической теплотехники наибольший интерес представляют гидродинамическое и тепловое подобия. При этом оперируют безразмерными комплексами, составленными из разнородных физических величин, которые получили название чисел подобия или критериев подобия. Часто критерии подобия называют по фамилиям ученых, внесших большой вклад в развитие науки и записывают двумя первыми буквами латинского написания фамилии. Так, отношение 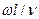называют критерием (числом подобия) Рейнольдса и обозначают Rе, а отношение 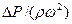называют критерием (числом подобия) Эйлера и обозначают Eu.

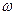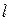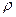В этих выражениях — скорость движения среды; — линейный размер (длина или диаметр); — коэффициент кинематической вязкости движущейся среды; — плотность движущейся среды; 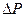— разность давлений между двумя интересующими исследователя точками.

Таким образом, условиями гидродинамического подобия является равенство критерия для агрегата (печи) и модели, т. е.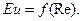

Так в результате экспериментального исследования на модели гидродинамической задачи, которую нельзя было решить ни математически, ни экспериментально непосредственно на агрегате, получают эмпирические выражения типа 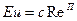, где с, п — коэффициенты, определенные из опыта.

Такие выражения пригодны для соответствующих расчетов как печи в целом, так и отдельных (исследованных на модели) ее элементов. Такая критериальная форма записи результатов экспериментального исследования обладает универсальностью. Предположим, что нас интересует зависимость разности давлений между двумя точками печи 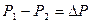от скорости движения среды 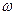, ее вязкости и расстояния между этими точками 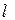. 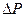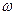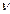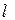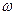Проводя такие исследования без использования критериальной записи, пришлось бы измерять перепад давлений , сначала изменяя величину при постоянных и , затем изменяя величину при постоянных и 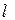и т. д.

Целесообразнее рассматривать зависимость перепада давлений 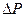от критерия Rе в целом. Ведь то же численное значение 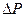возможно при различных комбинациях значени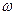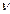й , и 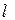. Следовательно, критериальная запись результатов эксперимента обеспечивает удобство и универсальность, так как достаточно изменять при проведении опытов значение Rе, чем охватывать всю область интересующих значени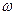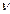й , и 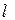, без поочередного их изменения.

Поэтому теорию подобия называют теорией эксперимента, подразумевая под этим возможность с применением теории подобия поставить достаточно точный и универсальный эксперимент, результатом которого явится эмпирическое уравнение, пригодное и удобное для практических расчетов.

Часто уравнение типа 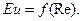используется для записи результатов экспериментов на действующих печах. Это позволяет распространить результаты экспериментов на ряд подобных печей других размеров.

Таким образом, теория подобия позволяет заменить математическое решение задачи экспериментальным. Это означает, что вместо формулы, полученной математическим решением системы уравнений, с применением теории подобия можно получить эквивалентную эмпирическую критериальную формулу. Применительно к задачам металлургической теплотехники это относится как к гидравлическому подобию, так и к тепловому подобию, которое рассматривается в другом блоке лабораторных работ и является основой при изучении широкого круга задач в области теплопередачи.

Моделирование

Моделирование в области механики газов с использованием положений теории подобия имеет ряд особенностей. Рассмотрим характер зависимости 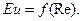. В некоторых случаях начиная с определенного значения Re критерий Eu перестаёт изменяться с изменением Re. Подобное значение критерия Re называют критическим. В области значений критерия Re выше критического при увеличении Re (иначе говоря, при возрастании скорости движения) характер движения не изменяется и поток (при различных Re) остается подобен сам себе, как бы моделирует сам себя. Такую область называют автомодельной областью. В автомодельной области достижение подобия возможно при неравенстве значений Rе образца и модели. В этом случае процессы в модели подобны процессам в образце при обеспечении в модели числа Rе, несколько меньшего, чем Re_КР. Понятие автомодельности широко используется в практике моделирования печей. Всякая модель печи создается в определенном геометрическом масштабе к образцу. Расход моделирующей среды (обычно воды или воздуха) определяется, исходя из равенства критериев 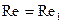из которого находят скорость движения среды в модели:

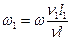. (1)

Если использовать величины масштаба вязкости 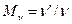и линейного масштаба , то .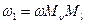

В автомодельной области при 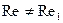; можно использовать понятие масштаба чисел Rе, т. е. .

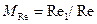При этом выражение для скорости движения среды в модели имеет вид

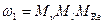. (2)

Т.к. 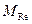обычно значительно меньше единицы, то скорость движения среды, подсчитанная по выражению (2), меньше значения, подсчитанного по выражению (1). Это обстоятельство является очень важным для практики моделирования, так как позволяет работать с меньшим расходом моделирующей среды, который равен 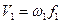,где 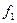— сечение модели, которому соответствует скорость .

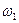Полученные на модели результаты (например, перепады давлений между выбранными точками) можно перенести на образец, используя равенство критериев Эйлера.