Нелинейные законы фильтрации

Проверке и исследованию пределов применимости закона Дарси посвящено значительное число работ отечественных и зарубежных специалистов. В процессе этих исследований показано, что можно выделить верхнюю и нижнюю границы применимости закона Дарси и соответствующие им две основные группы причин.

Верхняя граница определяется группой причин, связанных с проявлением инерционных сил при достаточно высоких скоростях фильтрации.

Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости, её взаимодействием с твёрдым скелетом пористой среды при достаточно малых скоростях фильтрации.

Рассмотрим каждый из этих предельных случаев, которые приводят к нелинейным законам фильтрации.

Верхняя граница применимости закона Дарси. Наиболее полно изучены отклонения от закона Дарси, вызванные проявлением инерционных сил при увеличении скорости фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением 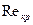числа Рейнольдса[2]

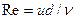, (II.21)

где 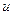- средняя скорость движения потока в порах; 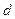— некоторый характерный линейный размер пористой среды (диаметр пор); 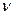- кинематический коэффициент вязкости флюида ( )

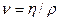Многочисленные экспериментальные исследования и, в частности, опыты Дж. Фэнчера, дж. Льюиса и К. Бернса, Линдквиста, Г. Ф. Требина, Н. М. Жаворонкова, М. Э. Аэрова и других были направлены на построение универсальной зависимости (по аналогии с трубной гидравликой) коэффициента гидравлического сопротивления 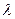. от числа Рейнольдса. Однако вследствие различной структуры и состава пористых сред получить такую универсальную зависимость не удается.

При обработке результатов экспериментов значительное внимание обращалось на такой выбор характерного размера поровой структуры, чтобы отклонения от закона Дарси возникали при одинаковых значениях числа Рейнольдса, и закон фильтрации в нелинейной области допускал универсальное представление.

Первая количественная оценка верхней границы применимости закона Дарси была дана более 60 лет назад Н. Н. Павловским, который, опираясь на результаты Ч. Слихтера, полученные для модели идеального грунта, и полагая характерный размер 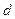равным эффективному диаметру 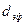, вывел следующую формулу для числа Рейнольдса

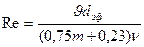. (II.22)

Использовав эту формулу и данные экспериментов, Н. Н. Павловский установил, что критическое значение числа Рейнольдса находится в пределах 7,5 < 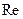<9.

Достаточно узкий диапазон изменения значений 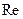, объясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.

Для удобства обработки результатов экспериментов различных авторов В. Н. Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси и определяемый равенством

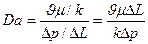(II.23)

Рис. 4. Зависимость параметра Дарси от числа Рейнольдса

Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Сравнивая равенство (II.23) и закон Дарси (II.17) (для случая горизонтального пласта, когда р^* = р), можно утверждать, что если справедлив закон Дарси, то

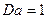. (II.24)

Таким образом, равенство (II.24) должно выполняться при 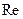< 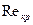Введение параметра 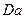упрощает исследование границы применимости линейного закона фильтрации. Действительно, если на оси абсцисс откладывать 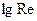, а по оси ординат - 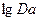, то поскольку 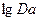= 0, при 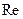< 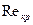графиком зависимости 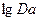от 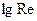будет прямая линия, совпадающая с осью абсцисс до тех пор, пока 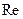< 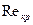. Как только на этом графике линия начнёт отделяться от оси абсцисс, сразу же обнаружится нарушение закона Дарси ( это соответствует значениям , Da<1, lgDa<0). Значение 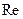, при котором станет заметно отклонение упомянутой линии от оси абсцисс, и будет критическим значением для иллюстрации сказанного на рис. 4 на логарифмической сетке приведены зависимости 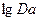от 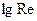, представляющие результат обработки опытов по формулам В. Н. Щелкачева (табл. II.1). Данные на этом графике соответствуют области нелинейной фильтрации (lgDa<0) для различных образцов пористых сред.

Основываясь на этих соображениях, В. Н. Щелкачев провел критический анализ и сравнение формул, полученных разными исследователями, для определения 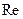в подземной гидромеханике и оценки возможных критических значений числа Рейнольдса 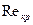, соответствующих верхней границе применимости закона Дарси. Результаты такого сопоставления приведены в табл. II.1. В первых двух строках таблицы даны соответственно формулы для 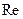и коэффициента гидравлического сопротивления 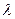, полученные разными авторами. В четвертой и пятой строках приведены соответственно критические значения 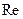, полученные самими авторами, и их уточнённые значения.

Наличие третьей строки табл. II.1, в которой дано произведение 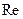объясняется следующим. В области линейного закона фильтрации ( 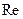< 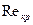) справедливо равенство II.24). Поэтому если произведение 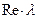зависит только от параметра 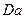(см. графы 5—8 табл. II.1), то оно имеет постоянное значение (не зависящее от свойств пористой среды) в случае, если 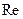< 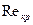. И только в этом случае можно получить <универсальный> прямолинейный график в координатах ( 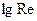, 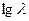), соответствующий фильтрации различных флюидов через различные по свойствам пористые среды. Результаты обработки опытов подтверждают этот вывод.

На основе анализа данных, приведенных в табл. 1, можно сделать следующие выводы.

1. Несмотря на отмеченные недостатки результатов Н. Н. Павловского, есть основания для их сопоставления с соответствующими результатами трубной гидравлики. Важно подчеркнуть, что критические значения числа Рейнольдса, подсчитанные по формуле (II.22), намного меньше тех, которые в трубной гидравлике соответствуют переходу ламинарного течения в турбулентное. Это служит одним из доводов в пользу того, что причины нарушения закона Дарси при высоких скоростях фильтрации (увеличение влияния сил инерции по мере увеличения 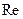) не следует связывать с турбулизацией течения. Отсутствие турбулентности при нарушении закона Дарси было доказано также прямыми опытами, изложенными Г. Шнебели.

Формулы Фэнчера, Льюиса и Бериса получены формальным введением в выражение для числа Рейнольдса эффективного диаметра 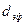в качестве характерного размера пористой среды, они не сопоставимы с результатами трубной гидравлики, дают слишком узкий диапазон изменения значений 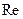(см. графу 4 табл.1), мало обоснованы.

2. Во все другие формулы табл. II.1 (графы 5—9) в качестве характерного размера входят величины, пропорциональные 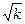, (где 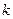— коэффициент проницаемости породы), методы определения которых хорошо известны. Формулы этой группы не имеют принципиальных преимуществ и одинаково удобны для практического использования. Для этих формул характерно то, что все они приводят к очень широким диапазонам изменения 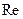для различных пористых сред. И это представляется вполне естественным ввиду разнообразия свойств испытанных пористых сред. Кроме того, это свидетельствует о том, что ни в одну из предложенных формул для определения 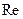не входит полный набор параметров, позволяющий характеризовать сложную структуру пористых сред, использования для этой цели коэффициентов пористости и проницаемости явно недостаточно.

Вместе с тем, широкий диапазон изменения значений 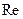, можно разбить на сравнительно узкие интервалы, соответствующие различным группам образцов пористых сред. Это облегчает указание возможной верхней границы справедливости закона Дарси при движении флюида в какой-либо пористой среде.

Результаты такого разбиения для формулы В. Н. Щелкачева (см. табл.1, первая строка, пятая графа) приведены в табл.2.

Таблица 1

Определение верхней границы применимости закона Дарси по данным различных исследований (в табл. 1 )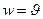

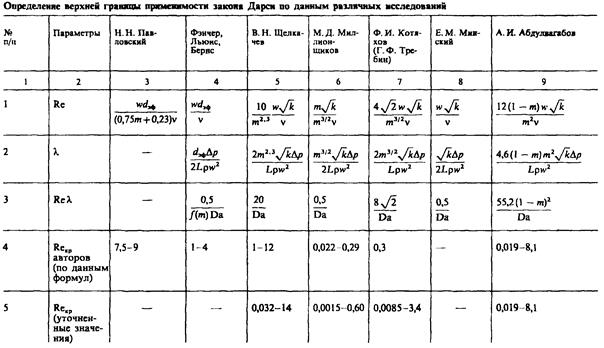
Таблица 2