Интервалы критических значений Re для различных образцов пористых сред

Итак, при значениях числа Рейнольдса 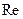> 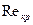линейный закон Дарси перестаёт быть справедливым. Первое обобщение закона Дарси на случай больших 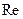, основанное на опытных данных, было выполнено Дюпюи, который сформулировал двучленый закон фильтрации, носящий имя австрийского исследователя Ф. Форхгеймера. независимо установившего его несколько позднее. В принятых сейчас обозначениях это соотношение можно представить (для простейшего случая прямолинейно-параллельного течения без учёта силы тяжести) в следующем виде:

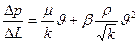, (II.25)

где 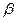- дополнительная константа пористой среды, определяемая экспериментально.

Первое слагаемое в правой части (II.25) учитывает потери давления вследствие вязкости жидкости, второе - инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов. Из (II.25) следует, что при малых скоростях фильтрации квадратом скорости 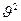можно пренебречь, и градиент давления будет зависеть только от первого слагаемого, т. е. движение будет безынерционным, соответствующим закону Дарси. При больших скоростях фильтрации силы инерции становятся существенными и будут сопоставимы или даже преобладать над силами вязкости.

Хорошая согласованность соотношения (II.25) с данными промысловых и экспериментальных наблюдений была установлена в многочисленных работах советских и зарубежных исследователей. Это свидетельствует о том, что данное соотношение представляет нечто большее, чем простую эмпирическую формулу, поскольку оно хорошо выполняется даже для весьма больших значений скорости фильтрации. Физический смысл этого заключается в том, что при больших скоростях быстропеременное движение в порах вследствие <извилистости> поровых каналов сопряжено с появлением значительных инерционных составляющих гидравлического сопротивления. С увеличением числа Рейнольдса квадратичный член в выражении (II.25) оказывается преобладающим, силы вязкости пренебрежимо малы по сравнению с силами инерции, и (II.25) сводится тогда к квадратичному закону фильтрации, предложенному А. А. Краснопольским. Он справедлив в средах, состоящих из частиц достаточно крупных размеров.