Скорость фильтрации. Закон Дарси

При изучении фильтрационного потока удобно отвлечься от размеров пор и их формы, допустив, что жидкость движется сплошной массой, заполняя весь объем пористой среды, включая пространство, занятое скелетом породы. Рассмотрим величину, называемую скоростью фильтрации.

Предположим, что объёмный расход жидкости в единицу времени через площадку 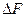, выделенную в пористой среде, равен .

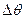Скорость фильтрации 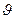в пределах данной площадки 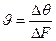. (II.3)

Скорость фильтрации в данной точке пласта 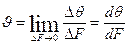. (II.4)

Установим связь между скоростью фильтрации 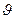и средней скоростью движения жидкости в порах .

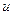Пусть 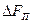— площадь просветов, находящихся на площадке 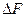; просветность 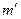определяется как следующее отношение: 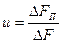. (II.5)

Если вычисляется средняя скорость движения в порах, то расчёт производится так:

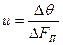. (II.6)

Подставив в (II.6) значение 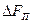из (II.5) и учитывая, что получим:

(II.7)

Такова зависимость между скоростью фильтрации и средней скоростью движения.

Скорость фильтрации можно рассматривать как вектор. Если в данной точке области фильтрации вращать элементарную площадку и восстанавливать нормали к ней, направление нормали, соответствующее наибольшему расходу, будет направлением вектора скорости фильтрации.

Рис. 3 Схема наклонного пласта.

В середине прошлого столетия в результате экспериментального изучения движения воды через песчаные фильтры был установлен основной закон фильтрации — закон Дарси (или линейный закон фильтрации). Этот закон является хронологически первым законом теории фильтрации. Его можно записать так:

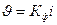, (II.8)

где К_ф — коэффициент фильтрации, имеющий размерность скорости; i — гидравлический уклон.

Коэффициент фильтрации К_ф зависит от свойств пористой среды и свойств фильтрующейся жидкости. Наибольшее влияние на этот коэффициент оказывают размеры частиц породы. Величина К_ф зависит также от формы частиц, степени шероховатости их поверхности, пористости среды, вязкости жидкости.

Видоизменим формулу (II.8).

Допустим, что в цилиндрической трубке, заполненной пористой средой, фильтруется жидкость в направлении, указанном стрелкой (рис. 3). Найдём потерю напора на данном участке длиной .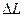

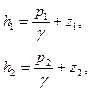Если пренебречь величиной скоростного напора, можем считать напоры 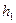и 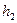равными соответственно:

(II.9)

где 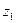и 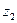— геометрические высоты крайних точек участка; 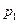и 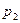— давления в этих точках; 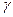— вес единицы объёма жидкости.

Потеря напора 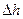запишется так: 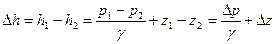, (II.10)

где 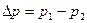— потеря давления, а .

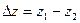Но гидравлический уклон 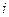можно с помощью формулы (II.10) записать так:

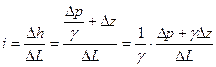. (II.11)

Подставив значение 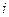из (II.11) в формулу (II.8), получим:

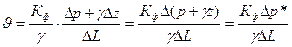, (II.12)

где 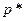— приведённое давление, причём 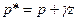. (II.13)

В случае горизонтального пласта в формуле (II.12) надо положить 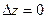; следовательно, закон Дарси запишется так: 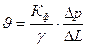. (II.14)

В символах дифференциального исчисления формула (II.14) (закон Дарси) имеет следующий вид:

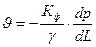, (II.15)

где 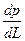— величина градиента давления, а знак минус в правой части показывает, что скорость фильтрации направлена в сторону понижения давления.

Итак, закон Дарси заключает в том, что скорость фильтрации пропорциональна градиенту давления.

Закон Дарси имеет силу, если соблюдаются следующие условия:

1) мелкозернистая пористая среда или достаточно узкие поровые каналы;

2) малая скорость фильтрации или небольшой градиент давления;

З) незначительные изменения скорости фильтрации или градиента давления.