Теплопроводность металлов.

Металлы в отличие от других твердых тел, как правило, являются хорошими проводниками теплоты и электричества. Согласно закону Видемана-Франца, установленному экспериментально, отношение теплопроводности c_е к удельной электропроводности s для большинства металлов пропорционально температуре Т, при этом коэффициент пропорциональности L (число Лоренца) одинаков для всех металлов:

c_е /s = LТ. (7.7)

Друде для объяснения такой закономерности положил, что основная часть теплового потока при наличии градиента температуры переносится электронами проводимости. Согласно модели Друде, металл представляется в виде ящика, заполненного свободными электронами, для которых справедливы законы кинетической теории газов. Для достижения электронейтральности металла считалось, что ящик заполнен соответствующим количеством положительно заряженных частиц, которые неподвижны. Электроны распределены по скорости в соответствии с функцией распределения Максвелла-Больцмана:

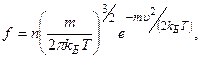(7.8)

где n - концентрация электронов. В соответствии с этим распределением электроны при температуре Т обладают всеми возможными значениями скоростей от 0 до + ¥, причем при отсутствии внешних сил все направления скоростей равновероятны и постоянно изменяются вследствие столкновений с положительно заряженными частицами. В промежутках между столкновениями взаимодействие электрона с другими электронами и ионами не учитывалось.

При вычислении удельной электропроводности предполагалось, что за единичное время электрон испытывает столкновения (изменяет направление скорости) с вероятностью, равной 1/t, где t- время релаксации, или время свободного пробега электрона. За время t электрон проходит расстояние между столкновениями, равное его средней длине свободного пробега <l_эл> = ut. Если к двум противоположным концам металла приложить разность потенциалов, создающую в каждой точке металла электрическое поле напряженности Е, то между двумя столкновениями электрон под действием силы: (e - заряд электрона) будет двигаться равномерно ускоренно. К концу промежутка времени t слагающая скорости в направлении вектора 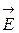изменится на . Так как после столкновения скорость электрона может иметь любые направления, то средняя скорость электронов в направлении поля 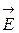равна среднему значению величины , т.е.

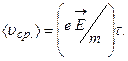(7.9)

Это среднее значение скорости в ускоренном движении называется дрейфовой скоростью(отношение 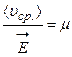- называют подвижностью электронов). Существование у всех электронов этой слагающей скорости с постоянным направлением выражается в том, что в направлении, обратном вектору, в металле происходит перемещение отрицательного заряда. При этом плотность тока можно вычислить, пользуясь выражением:

(7.10)

С другой стороны, согласно закону Ома, плотность тока:

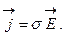(7.11)

Отсюда следует, что удельная электропроводность При расчете теплопроводности предполагается, что при наличии градиента температуры электроны от столкновения до столкновения проходят одинаковые расстояния, равные средней длине свободного пробега 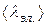, прежде чем передают свою избыточную тепловую энергию атомам. Применяя к электронному газу представления кинетической теории газов, получим для теплопроводности выражение

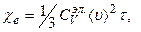(7.12)

где С_v^эл - теплоемкость электронного газа; <u> - средняя скорость электронов. Если записать отношение электронной теплопроводности к его удельной электропроводности 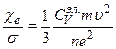, положив С_v^эл = 3Nk_Б/2 и mu²/2 = 3k_БT/2, получим закон Видемана-Франца

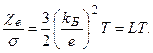(7.13)

Постоянная L = 2,45×10^-8 Вт×Ом/К² не зависит от сорта металла и носит название числа Лорентца. Число Лорентца, полученное по теории Друде, сильно отличается от экспериментельного значения. Это связано с тем, что теория Друде требует большого числа электронов для объяснения электропроводности и малого – для объяснения теплоемкости.

Зоммерфельд, сохранив основные исходные положения теории, применил квантовую статистику Ферми-Дирака, так как для электронов, подчиняющихся принципу запрета Паули, распределение Максвелла-Больцмана должно быть заменено распределением Ферми-Дирака

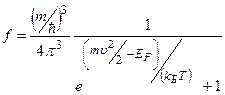. (7.14)

Тогда

где L = 2,45×10^-8 Вт×Ом/К², что находится в согласии с экспериментальными данными.

В общем случае теплопроводность металлов складывается из теплопроводности, обусловленной фононами, и теплопроводности, обусловленной свободными электронами:

c=c_реш. + c_е (7.15)

В металлах теплопроводность, обусловленная фононами, в 100 раз ниже теплопроводности, обусловленной электронами.