ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО

РЕШЕНИЯ

6.1. Удельная теплоемкость алюминия при 20⁰С равна 896 Дж/(кг К). Выполняется ли при этой температуре для него закон Дюлонга и Пти?

ОТВЕТ: не выполняется.

6.2. Удельные теплоемкости свинца и алюминия при постоянном объеме и температуре 20⁰С составляют соответственно 126 и 896 Дж/(кг К). Молярная масса свинца равна 207,21 г/моль, алюминия – 26,99 г/моль. Вычислить теплоемкости одного моля для каждого из них и сравнить со значениями, полученными по закону Дюлонга и Пти.

ОТВЕТ: С_{v Al} = 24,17 Дж/моль×град; C_{v Pb}= 26,1 Дж/моль×град.

6.3. Рассчитать значение теплоемкости твердого тела по теории Эйнштейна.

ОТВЕТ: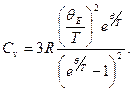

6.4. Имеется система N молекул, которые могут находиться в двух различных энергетических состояниях, отличающихся друг от друга значением энергии DЕ. Определить теплоемкость такой системы.

ОТВЕТ: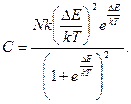

6.5. Почему электронная теплоемкость неметаллов практически равна нулю?

6.6. Показать, что теплоемкость по теории Дебая достигает значения 3R при высоких температурах, когда q_Д/Т ®0.

6.7. Показать, что при низких температурах теплоемкость твердого тела по теории Дебая пропорциональна кубу абсолютной температуры.

6.8. Характеристическая температура золота 170 К. Определить постоянную квазиупругой силы. Молярная масса золота равна 197,2 г/моль.

ОТВЕТ: ¡ = 88,7 кг/сек².

6.9. Теплоемкость серебра при 10К равна 199 Дж/(кмоль К). Определить характеристическую температуру.

ОТВЕТ: q = 213 К.

6.10. Найти в общем случае разность теплоемкостей тела при постоянном давлении и постоянном объеме.

ОТВЕТ: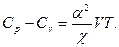

6.11. С помощью общих термодинамических соотношений установить связь между коэффициентом объемного расширения, объемной сжимаемости и термической упругостью твердого тела.

ОТВЕТ: a/c = gР.

6.12. Показать, что при низких температурах коэффициенты термического расширения кристаллов стремятся к нулю.

6.13. Определить изменение внутренней энергии кристалла никеля при нагревании от температуры 0⁰С до 200⁰С. Масса кристалла составляет 10 г, молярная масса равна 58,69 г/моль.

ОТВЕТ: 1,70 кДж.

6.14. Определить теплоту, необходимую для нагревания кристалла NaCl массой m = 10 г на DТ = 1К. Рассмотреть два случая:

1) нагревание происходит от температуры Т₁ = q_Д;

2) нагревание происходит от температуры Т₂ = 1К.

Характеристическую температуру Дебая для NaCl принять равной 320К. Молярная масса натрия равна 22,99 г/моль, хлора 35,45 г/моль.

ОТВЕТ: Dq₁ = 4,08 Дж; Dq₂ = 38 мкДж.

6.15. Показать, что если смещение частиц в кристаллической решетке твердого тела подчиняется закону Гука F(x) = - b x, то тепловое расширение отсутствует.

6.16. Определить энергию и теплоемкость системы, состоящей из N = 10²⁵ классических трехмерных независимых гармонических осцилляторов. Температура Т = q_Д =300 К.

ОТВЕТ: 124 кДж; 414 Дж/К.

6.17. Определить энергию системы, состоящей из N= 10²⁵ квантовых трехмерных независимых осцилляторов при температуре Т = q_Е = 300 К.

ОТВЕТ: 72,2 кДж.

6.18. Используя квантовую теорию теплоемкости Эйнштейна, вычислить изменение внутренней энергии одного моля кристалла при нагревании его на DТ =2К от температуры Т = 1/2 q_Е.

ОТВЕТ: 36 Дж.

6.19. Определить максимальную частоту собственных колебаний в кристалле золота по теории Дебая. Характеристическая температура золота q_Д = 180К.

ОТВЕТ: 2,37×10¹³ Гц.

6.20. Используя квантовую теорию теплоемкости Дебая, вычислить изменение внутренней энергии одного моля кристалла при нагревании его на DТ = 2К от температуры Т = 1/2 q_Д.

ОТВЕТ: 484,7 Дж.

6.21. Пользуясь теорией теплоемкости Дебая, определить изменение внутренней энергии одного моля кристалла при нагревании его от нуля до Т = 0,1q_Д. Характеристическую температуру Дебая принять равной 300К, считать, что Т<<q_Д.

ОТВЕТ: 14,54 Дж.

6.22. Вычислить по теории Дебая нулевую энергию одного моля кристалла меди. Характеристическая температура q_Д для меди равна 320К.

ОТВЕТ: 2,2×10^-21 Дж.

6.23. Какова удельная теплоемкость цинка при 100⁰С? Молярная масса цинка равна 65,38 г/моль.

ОТВЕТ: 0,382×10^-3 Дж/кг×К.

6.24. Найти коэффициент объемного расширения В для анизотропного кристалла, коэффициенты линейного расширения которого по трем взаимно перпендикулярным направлениям составляют a₁= 1,25 10^-5К^-1; a₂=1,10 10^-5 К^-1; a₃=1,15 10^-5 К^-1.

ОТВЕТ: 3,40×10^-5 К^-1.

6.25. Вычислить по теории Эйнштейна нулевую энергию, которой обладает один моль кристалла цинка. Характеристическая температура q_Е для цинка равна 230К.

ОТВЕТ: 2,2×10^-21 Дж.

6.26. Вычислить среднюю длину свободного пробега фононов в кварце при некоторой температуре, если при той же температуре коэффициент теплопроводности l = 13 Вт/(м К), молярная теплоемкость С_m = 44 кДж/(кмоль К) и усредненной значение скорости звука <u> = 5000 м/с, плотность кварца r = 2,65 10³ кг/м³.

ОТВЕТ: 4,0 нм.

6.27. Каково максимальное изменение потенциальной энергии атомов в кристаллической решетке твердого тела при гармонических колебаниях, если амплитуда тепловых колебаний тела составляет 5% среднего межатомного расстояния. Среднее межатомное расстояние принять равным 0,3 нм, модуль Юнга Е = 100 Гпа.

ОТВЕТ: 3,4 ×10^-21Дж.

6.28. Вычислить электронную теплоемкость для меди при температуре 2 и 1000К и сравнить ее с теплоемкостью решетки при тех же температурах. Характеристическая температура меди равна 316К, g = 6,95×10^-4 Дж/моль×К.

ОТВЕТ: 1). С_vэл = 14,56×10^-4 Дж/моль×град; С_vэл = 0,728 Дж/моль×град; С_vр = 4,8×10^-4 Дж/моль×град; С_vр = 24,96 Дж/моль×град.