РАЗДЕЛ 7. Электроны в металлах. Свободный электронный газ Ферми

Основываясь на модели свободных электронов, можно объяснить целый ряд важных физических свойств металлов.Внимания заслуживают следующие свойства металлов:

1. В изотермических условиях в металле хорошо выполняется закон Ома, связывающий плотность тока J с напряженностью электрического поля Е через скалярную электропроводность s: .

2. Металл очень хороший проводник электричества (электропроводность металла составляет ~ (10⁶¸10⁸) Ом^-1×м^-1.

3. Металл обладает высокой электронной теплопроводностью c_е. Видеман и Франц заметили, что хороший проводник тепла одновременно является и хорошим проводником электричества. Совпадение отношения (c_е/s) для разных металлов при данной температуре носит название закона Видемана-Франца. Лоренц заметил, что отношение (c_е/sТ) не зависит от температуры и имеет одинаковую величину для многих металлов, поэтому величину L º (c_е/sТ) называют числом Лоренца.

4. Если металл охлажден ниже некоторой характеристической температуры, связанной с температурой Дебая q_Д для теплоемкости, то наблюдается рост c_е и еще большее возрастание s.

5. При достаточно низкой температуре электропроводность s достигает насыщения, и ее значение при этом определяется примесями и дефектами решетки.

6. Магнитные эффекты в ферромагнитных металлах и сплавах также дают вклад в электрическое удельное сопротивление.

7. Примерно половина металлических элементов при достаточно низких температурах становятся сверхпроводниками.

8. Газ свободных электронов обладает очень малой удельной теплоемкостью, которая пропорциональна абсолютной температуре, а также очень малой магнитной восприимчивостью, которая не зависит от температуры.

9. При наличии комбинации электрического, магнитного и температурного градиентов возникают многочисленные термо-гальвано-магнитные эффекты.

10. В очень чистых монокристаллах в сильно магнитных полях проявляются эффекты, зависящие от ориентации; их величина обнаруживает осциллирующую зависимость от напряженности магнитного поля.

Модель свободных электронов предполагает, что внешние электроны в металле могут довольно свободно перемещаться в объеме кристаллической решетки. Эти валентные электроны называют электронами проводимости, так как они становятся носителями электрического тока в металле. В основу модели свободных электронов положены упрощения, основными из которых являются:

1. Не учитывается влияние положительно заряженных ионов на движение электронов в промежутках между столкновениями;

2. Отсутствие взаимодействия электронов между собой. Это свойство электронов является следствием принципа Паули. Согласно принципу Паули электрон, находящийся в заполненной оболочке данного атома, должен быть связан исключительно с этим атомом.

Газ свободных, невзаимодействующих электронов, подчиняющихся принципу Паули, называют свободным электронным газом Ферми. Полную энергию электронов можно считать равной их кинетической энергии, а потенциальной можно пренебречь. Энергия Ферми e_F определяется как энергия электронов на высшем еще заполненном уровне. В одномерном случае

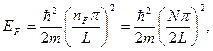(7.1)

где n_F - квантовое число наивысшего занятого энергетического уровня; N = 2n_F - число электронов; m - масса электрона; L - длина отрезка прямой линии, ограничивающей движение электрона (на краях этого отрезка имеются бесконечной высоты потенциальные барьеры). При повышении температуры кинетическая энергия электронного газа увеличивается. При этом некоторые энергетические уровни, которые при абсолютном нуле были вакантными, оказываются занятыми, и одновременно часть уровней, которые при абсолютном нуле были заняты, становятся вакантными. Вероятность того, что в состоянии теплового равновесия идеального электронного газа при температуре Т состояние с энергией e занято электронами есть функция распределения Ферми-Дирака

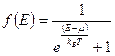, (7.2)

где m - химический потенциал. m - это максимальная энергия, которую могут иметь электроны проводимости в металле при абсолютном нуле температуры: m=e_F (f(E) = 1/2). Наивысший уровень, занятый электронами, называется уровнем Ферми.Ему соответствует энергия Ферми E_F, которую имеет электрон на этом уровне.

Закон распределения электронов проводимости по энергиям при Т = 0К имеет вид

(7.3)

Общее число электронов проводимости в единице объема металла

(7.4)

Отсюда: Средняя энергия электрона <Е> при Т = 0К

(7.5)

Cкорость электронов на поверхности Ферми равна

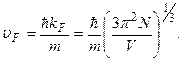
(7.6)

k_F - радиус сферической области, заполненной электронными состояниями в k-пространстве. Число состояний на единичный энергетический интервал g(E) называется плотностью состояний 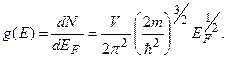Число состояний на единичный энергетический интервал вблизи энергии Ферми равно отношению числа электронов проводимости к энергии Ферми g(E_F) = 3N/2E_F.