РАЗДЕЛ 6. Тепловые свойства твердых тел

Атомы в твердом теле при любой температуре совершают тепловые колебания около своих средних положений равновесия. При нагревании твердого тела, поглощаемая им теплота расходуется на увеличение интенсивности теплового движения. Основные особенности теплового движения в твердых телах отслеживают по поведению теплоемкости с изменением температуры. Теплоемкость С_v твердого тела при постоянном объеме выражает изменение тепловой энергии при изменении температуры тела на 1⁰С и находится дифференцированием Е_реш по Т: С_v=dЕ_реш/dT. Тепловая энергия Е_реш складывается из энергии нормальных колебаний решетки. Умножая число нормальных колебаний, приходящихся на спектральный участок dw, равное g(w)dw, на среднюю энергию нормального колебания 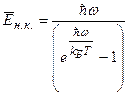, получим энергию нормальных колебаний, заключенных в интервале dw: dE_реш= 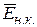g(w)dw. Проинтегрировав это выражение по всему спектру нормальных колебаний, т.е. в пределах от 0 до w_Д, получим энергию тепловых колебаний решетки твердого тела:

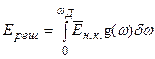. (6.1)

Основным вопросом теории теплоемкости является зависимость С_v от температуры. Рассмотрим вопрос о зависимости С_v от температуры для двух областей температур: область низких температур Т << q_Д (q_Д - температура Дебая) и область высоких температур Т > q_Д.

1. Область высоких температур.

В области высоких температур изменение энергии твердого тела может происходить только за счет повышения степени возбуждения нормальных колебаний, приводящего к увеличению их средней энергии. Полная средняя тепловая энергия системы, состоящей из N_a атомов с 3N_a степенями свободы равна Е = 3N_ak_бТ. Отсюда молярная темплоемкость

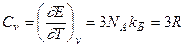. (6.2)

Здесь N_A = 6,022 10²³ моль^-1- постоянная Авогадро; k_Б = 1,38 10^-23Дж/К - постоянная Больцмана; R = 8,31 Дж/моль К - молярная газовая постоянная. Это закон Дюлонга и Пти, достаточно хорошо оправдывающийся на практике.

2. Область низких температур.

В области низких температур энергия кристалла с повышением температуры увеличивается вследствие действия двух механизмов:

1) роста средней энергии каждого нормального колебания из-за повышения степени его возбуждения;

2) роста числа возбужденных нормальных колебаний решетки.

Первый механизм вызывает рост энергии, пропорциональный Т, второй - пропорциональный - Т³. Поэтому в целом с повышением температуры энергия решетки растет пропорционально Т⁴: Е_реш ~ Т⁴, а теплоемкость пропорционально Т³ (закон Дебая).

Физическая картина характера изменения температурной зависимости энергии и теплоемкости твердого тела при повышении его температуры выглядит таким образом. В области низких температур (Т<<q_Д) энергия тела с увеличением температуры повышается, во-первых, вследствие роста степени возбуждения каждого нормального колебания, т.е. роста их средней энергии, пропорциональной Т; во-вторых, вследствие включения в работу все новых и новых нормальных колебаний, вызывающих повышение энергии тела пропорционально Т³. По мере приближения к температуре Дебая второй механизм постепенно из работы выключается, и зависимость Е от Т ослабляется, что вызывает отступление от закона Дебая.

При температуре Дебая возбуждается уже весь спектр нормальных колебаний решетки, поэтому второй механизм роста энергии с повышением температуры выключается полностью; работает лишь первый механизм, вызывая рост энергии, пропорциональный Т, и независимость от Т темплоемкости тела С_v (закон Дюлонга и Пти).

Более строгие количественные расчеты, подкрепляющие качественные закономерности изменения С_v(Т), были выполнены в 1907г. Эйнштейном, а затем Дебаем (в 1912 г.).

1. Модель Эйнштейна.

Эйнштейн исходил из двух предположений:

- твердое тело представляет собой совокупность одинаковых гармонических осцилляторов (атомов), которые колеблются независимо друг от друга с одной и той же частотой w в трех взаимно перпендикулярных направлениях;

- энергия осцилляторов квантована по Планку.

Энергия Е системы из N_A атомов, определяемая колебаниями решетки равна

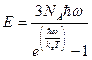. (6.3)

Тогда темплоемкость

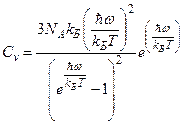. (6.4)

В области высоких температур формула (6.3) приобретает вид закона Дюлонга и Пти. В области низких температур С_v ~ 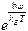. Ограниченность модели Эйнштейна состоит в его предположении о равенстве частот всех упругих волн в твердом теле.

2. Модель Дебая.

Дебай сохранил идею Эйнштейна о квантованности энергии гармонических осцилляторов по Планку, пополнив ее предположением о том, что гармонические осцилляторы колеблются с различными частотами. Энергия системы осцилляторов с различными частотами равна

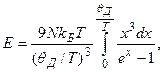(6.5)

где х = 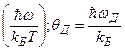. Тогда при высоких температурах теплоемкость: С_v = 3R, а при низких:

.

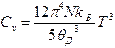Теплоемкость металлов складывается из темплоемкости решетки С_реш и теплоемкости электронного газа С_е

С_v = С_реш + С_е. (6.6)

С классической точки зрения (электронный газ невырожденный)

.

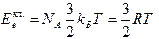Поэтому теплоемкость электронного газа С_е^кл = 3R/2, а общая теплоемкость С_v = 9R/2. В действительности в области высоких температур металлы, как и диэлектрики, обладают теплоемкостью С_v = 3R, что свидетельствует о том, что электронный газ не вносит заметного вклада в теплоемкость металлов. Это обстоятельство нашло объяснение в квантовой теории. Вследствие того, что электронный газ в металлах является вырожденным, термическому возбуждению даже в области высоких температур подвергается лишь незначительная доля свободных электронов (£ 10%); остальные электроны теплоту не поглощают. Поэтому теплоемкость такого газа незначительна по сравнению с теплоемкостью решетки и теплоемкость металла в целом практически равна теплоемкости его решетки. В области низких температур теплоемкость решетки падает ~ Т³ и вблизи абсолютного нуля может оказаться столь малой, что основное значение может приобрести теплоемкость электронного газа С_е, которая с понижением температуры падает значительно медленнее (С_е ~ T).

С нагреванием твердого тела средние расстояния между частицами увеличиваются, и тело расширяется. Причиной этого является ангармонический характер колебаний частиц твердого тела, обусловленный асимметрией кривой зависимости энергии взаимодействия частиц от расстояния между ними. Коэффициент линейного теплового расширения a равен

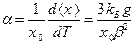, (6.7)

где <x> - среднее расстояние между атомами; х₀ - положение равновесия атомов, g - коэффициент ангармоничности, b - коэффициент квазиупругой силы.

Еще одним эффектом, обусловленным ангармоническим характером колебания атомов, является тепловое сопротивление твердых тел. Выражение для теплопроводности в случае фононов: К=1/3 (Сu L), где С - теплоемкость единицы объема, u - средняя скорость частицы, L-средняя длина свободного пробега между двумя последующими столкновениями. Теплопроводность металлов складывается в общем случае из теплопроводности, обусловленной фононами, и теплопроводности, обусловленной свободными электронами: К= К_реш.+К_эл., при этом для металлов К_эл./К_реш.=10².