Определить величину квазиимпульса фонона соответствующего частоте

Пример 1. Определить величину квазиимпульса фонона соответствующего частоте w = 0,1w_max. Усредненное значение скорости звука в кристалле = 1380 м/с, характеристическая температура Дебая q_Д = 100К. Дисперсией звуковых волн в кристалле пренебречь.

РЕШЕНИЕ.

Квазиимпульс фонона может быть вычислен по формуле:

.

При отсутствии дисперсии звуковых волн волновое число может быть определено из формулы 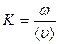. Тогда импульс фонона можно записать в виде

.

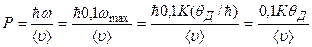Здесь учтено, что 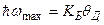. Подставив числовые значения, получим

Р = .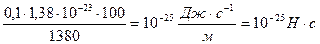

ОТВЕТ: Р = 10^-25 Н×с.

Пример 2: Период решетки а одномерного кристалла (т.е. кристалла, атомы которого образуют цепи, не взаимодействующие друг с другом) равен 3Å. Определить максимальную энергию фононов, распространяющихся вдоль этой цепочки атомов. Скорость звука в кристалле равна 5000 м/с.

РЕШЕНИЕ.

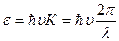Энергия фонона может быть найдена по формуле: . Частота w выражается через скорость фонона и его волновое число таким образом: w = uK (т.к. u = e/R = w/K). Тогда энергия будет равна: . Энергия будет максимальна при минимально возможном значении длины волны. Для одномерной цепочки l_min = 2а. Тогда

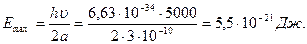
ОТВЕТ: Е_max = 5,5×10^-21 Дж.