Примеры решения задач. Найти выражение для коэффициента Пуассона

Пример 1. Кубический кристалл подвергнут растяжению в направлении [100]. Найти выражение для коэффициента Пуассона через упругие постоянные или модули упругости.

РЕШЕНИЕ.

Закон Гука для анизотропного тела записывается таким образом:

S₁ = s₁₁T₁ + s₁₂T₂ + s₁₃T₃ + s₁₄T₄ + s₁₅T₅ + s₁₆T₆;

S₂ = s₂₁T₁ + s₂₂T₂ + s₂₃T₃ + s₂₄T₄ + s₂₅T₅ + s₂₆T₆;

S₃ = s₃₁T₁ + s₃₂T₂ + s₃₃T₃ + s₃₄T₄ + s₃₅T₅ + s₃₆T₆;

S₄ = s₄₁T₁ + s₄₂T₂ + s₄₃T₃ + s₄₄T₄ + s₄₅T₅ + s₄₆T₆;

S₅ = s₅₁T₁ + s₅₂T₂ + s₅₃T₃ + s₅₄T₄ + s₅₅T₅ + s₅₆T₆;

S₆ = s₆₁T₁ + s₆₂T₂ + s₆₃T₃ + s₆₄T₄ + s₆₅T₅ + s₆₆T₆;

Для кубического кристалла закон Гука записывается таким образом:

S₁ = s₁₁T₁ + s₁₂T₂ + s₁₂T₃;

S₂ = s₁₂T₁ + s₁₁T₂ + s₁₂T₃;

S₃ = s₁₂T₁ + s₁₂T₂ + s₁₁T₃;

S₄ = s₄₄T₄;

S₅ = s₄₄T₅;

S₆ = s₄₄T₆;

Если существуют напряжения растяжения только вдоль оси [100], то лишь Т₁¹0. Тогда

S₁ = s₁₁T₁; S₂ = s₁₂T₁; S₃ = s₁₂T₁. Так как коэффициент Пуассона n = - S₂/S₁, то следует, что n = - s₁₂/s₁₁.

ОТВЕТ: n = - s₁₂/s₁₁.

Пример 2: Кубический кристалл подвергнут гидростатическому сжатию. Показать, что величина обратная сжимаемости В = - V(dP/dV), связана с упругими постоянными соотношением В = (с₁₁+2с₁₂)/3.

РЕШЕНИЕ.

В общем случае закон Гука для анизотропного тела записывается следующим образом: S_q = s_qrT_r (q, r = 1, 2, 3, 4, 5, 6), где S_q - компоненты тензора деформации, T_r - компонетнты тензора напряжения. При гидростатическом сжатии Т₁ = Т₂ = Т₃ = - Р и Т₄ = Т₅ = Т₆ = 0. Тогда закон Гука перепишется таким образом:

S₁ = - (s₁₁+s₁₂+s₁₃) P,

S₂ = - (s₁₂+s₂₂+s₂₃) P,

S₃ = - (s₁₃+s₂₃+s₃₃) P,

S₄ = - (s₁₄+s₂₄+s₃₄) P,

S₅ = - (s₁₅+s₂₅+s₃₅) P,

S₆ = - (s₁₆+s₂₆+s₃₅) P.

Объемная деформация определяется суммой S₁+S₂+S₃. Тогда

S₁ + S₂ + S₃ = - [s₁₁ + s₂₂ + s₃₃ + 2(s₁₂+s₂₃+s₁₃)] P.

Так как для кубических кристаллов s₁₁ = s₂₂ = s₃₃ и s₁₂ = s₂₃ = s₁₃, то сжимаемость

æ = - (S₁+S₂+S₃)/ Р = 3 (s₁₁+2s₁₂).

Поскольку с₁₁ + 2с₁₂ = 1/( s₁₁+2s₁₂), то В = 1/ æ = (с₁₁+2с₁₂)/3.

ОТВЕТ: В = (с₁₁+2с₁₂)/3.

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО

РЕШЕНИЯ

4.1. Показать, что скорость u волны сдвига, распространяющейся вдоль направления [110], когда частицы колеблются в направлении в кубическом кристалле, равна , где r - плотность кристалла.

4.2. Найти соотношение между модулями упругости и упругими податливостями кубического кристалла.

ОТВЕТ: С₁₁ = 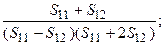C₁₂ = C₄₄ = .

4.3. Упругие постоянные бериллия С₁₁, С₃₃, С₄₄, С₁₂, С₁₃ соответственно равны: 30,8×10¹⁰; 35,7×10¹⁰; 11,0×10¹⁰; -5,8×10¹⁰ и 8,7×10¹⁰ Н/м². Бериллий имеет гексагональную решетку, для которой набор постоянных упругой жесткости сводится к матрице

.

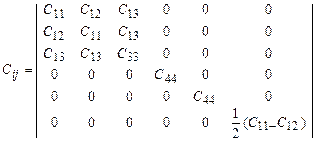Вычислить коэффициенты податливостей.

ОТВЕТ: S₁₁ » 0,37×10^-11 м²/Н; S₁₂ » 0,11× 10^-11 м²/Н; S₁₃ » - 0,11× 10^-11 м²/Н; S₃₃ » 0,34× 10^-11 м²/Н; S₄₄ » 0,9× 10^-11 м²/Н.

4.4. Податливости никеля (кубическая решетка) S₁₁, S₁₂, S₄₄ при комнатной температуре соответственно равны 0,799×10^-11; - 0,312×10^-11 и 0,84×10^-11 м²/Н. Определить модуль Юнга и модуль сдвига никеля в направлении [210].

ОТВЕТ: Е » 1,87×10¹¹ Н/м²; G » 0,79×10¹¹Н/м².

4.5. Определить модули упругости С₂₂,С₄₄, С₆₆ и С₄₆ моноклинного кристалла по скоростям распространения ультразвуковых волн, приведенных в таблице. Плотность кристалла 1160 кг/м³.

ОТВЕТ: С₂₂ » 9,7×10⁹ Н/м²; С₄₄ » 3,3×10⁹ Н/м²; С₆₆ » 2,4×10⁹ Н/м²; С₄₆ » 1,39×10⁹ Н/м².

4.6. Сжимаемость меди 0,76×10¹¹ м²/Н. Определить характеристическую температуру меди, если постоянная решетки 3,61 Å.

ОТВЕТ: q » 342 К.

4.7. Сжимаемость меди 0,76×10¹¹ м²/Н, коэффициент Пуассона 0,334. Определить характеристическую температуру меди. Сравнить это значение характеристической температуры со значением, полученным в предыдущей задаче.

ОТВЕТ: q » 342 К.

4.8. Резонансная частота цилиндрического никелевого стержня длиной 10 см и диаметром 0,442 см равна 1880 Гц. Определить модуль Юнга и модуль сдвига никеля, если плотность его 8800 кг/м³.

ОТВЕТ: Е » 2050 кГ/м²; G » 1268 кГ/м².

4.9. Показать, что скорость продольной волны, распространяющейся в направлении [111] в кубическом кристалле, равна 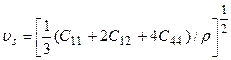. Для такой волны u=u=w. Положить:

.

4.10. Показать, что скорость поперечных волн, распространяющихся в направлении [111] в кубическом кристалле, равна 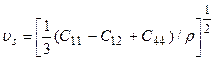. Использовать задачу 4.9.