ВИДЫ СРЕДНИХ ВЕЛИЧИН
Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания ее типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений, как правило, исчисляется система средних показателей. Так, например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др.
Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе научного способа расчета.
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.
Перечисленные средние относятся к классу степенных средних и объединяются общей формулой (при различных значениях т):
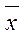 =
= 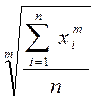 , (1)
, (1)
где 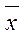 — среднее значение исследуемого явления;
— среднее значение исследуемого явления;
т — показатель степени средней;
x 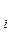 — текущее значение (вариант) осредняемого признака;
— текущее значение (вариант) осредняемого признака;
п — число признаков.
Далее пределы суммирования не указываются.
В зависимости от значения показателя степени т различают следующие виды степенных средних:
при m = -1 – средняя гармоническая 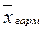 ;
;
при m = 0 – средняя геометрическая 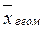 ;
;
при m = 2 – средняя арифметическая 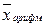 ;
;
при m = 3 – средняя кубическая 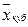 ;
;
При использовании одних и тех же исходных данных, чем больше т в формуле (1), тем больше значение средней величины:
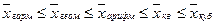
Это свойство степенных средних называется свойством мажорантности средних.
Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид средней выбирается в каждом отдельном случае путем конкретной анализа изучаемой совокупности, он определяется материальным содержанием изучаемого явления, а также принципам суммирования и взвешивания.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняясчитается по несгруппированным данным и имеет следующий общий вид:
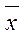 =
= 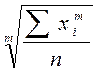 ,
,
где x 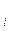 — варианта (значение) осредняемого признака;
— варианта (значение) осредняемого признака;
m — показатель степени средней;
n— число вариант.
Взвешенная средняясчитается по сгруппированным данным и имеет общий вид:
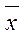 =
= 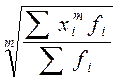 ,
,
где x 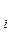 — варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
— варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
m — показатель степени средней;
f 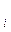 — частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
— частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
Для характеристики величины варьирующего признака пользуются так называемыми структурными средними:
· модой;
· квантилями распределения (медианой, квартили, децили и др.)
Квантиль – это значение признака Х, занимающее определенное место в упорядоченной по данному признаку совокупности.
Виды квантилей:
1) медиана(Ме) – значение признака, приходящегося на середину упорядоченной совокупности. Медиана делит ряд на две равные части;
2) квартили (Q 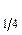 , Q
, Q 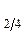 ,= Ме, Q
,= Ме, Q 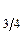 ) – значения признака, делящие упорядоченную совокупность на 4 равные части;
) – значения признака, делящие упорядоченную совокупность на 4 равные части;
3) децили (Q 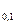 , Q
, Q 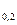 ,…, Q
,…, Q 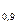 ) – значения признака, делящие упорядоченную совокупность на 10 равных частей;
) – значения признака, делящие упорядоченную совокупность на 10 равных частей;
4) процентили (Q 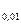 , Q
, Q 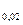 ,…, Q
,…, Q 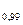 )– значения признака, делящие упорядоченную совокупность на 100 равных частей;
)– значения признака, делящие упорядоченную совокупность на 100 равных частей;
Мода(Мо 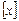 ) – это наиболее часто встречающееся значение признака совокупности. Мода применяется, например, при определении размера одежды, обуви, пользующихся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар на рынке и т.д.
) – это наиболее часто встречающееся значение признака совокупности. Мода применяется, например, при определении размера одежды, обуви, пользующихся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар на рынке и т.д.
Для дискретного ряда мода – это значение признака, которому соответствует наибольшая частота (частость) распределения. Для интервального ряда это значение признака, которому соответствует наибольшая плотность распределения. Если ряд равноинтервальный, то значение моды можно определить по частям (частостям): их соотношение будет таким же, что и плотностей распределения.
Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды. Если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным; если таких вариантов больше двух, то ряд – полимодальный.
Мода так же, как и медиана, не требует знания всех индивидуальных значений признака и поэтому может быть использована в качестве наиболее типичного значения признака в неоднородной совокупности.
Дата добавления: 2016-06-18; просмотров: 2682;











