Кривые второго порядка

Кривые второго порядка на плоскости определяются алгебраическими уравнениями второго порядка.

Эллипс

Эллипсомназывается геометрическое место точек M(x,y), для которых сумма расстояний до двух заданных точек F₁(+с,0) и F₂(-с,0) (называемых фокусами эллипса) постоянна и равна 2а.

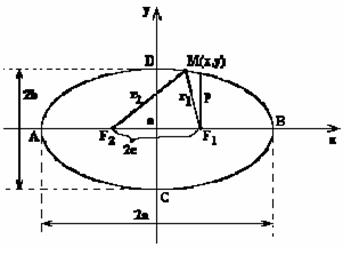
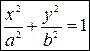− каноническое уравнение эллипса.

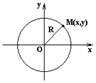
Окружность представляет собой геометрическое место точек, равноудаленных от точки О, называемой центром окружности. Уравнение окружности можно получить из уравнения эллипса при a=b=R:

x²+y²=R² − каноническое уравнение окружности.

Гипербола

Гиперболойназывается геометрическое место точек M(x,y), для которых абсолютная величина разности расстояний до двух заданных точек F₁(+c,0) и F₂(-c,0) (называемых фокусами гиперболы) постоянна и равна 2а.

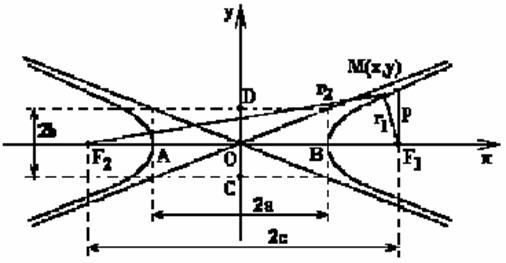
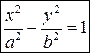− каноническое уравнение гиперболы.

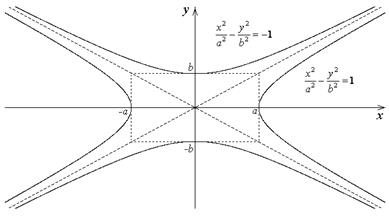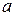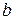Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениям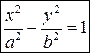и

и .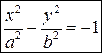

Сопряженные гиперболы имеют общие асимптоты. Действительная ось каждой из них есть мнимая ось другой и наоборот.

Парабола

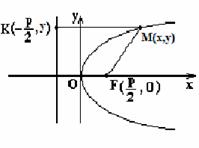Параболойназывается геометрическое место точек M(x,y), расстояние которых до определенной точки F(p/2,0) (называемой фокусом параболы) равно расстоянию до определенной прямой (называемой директрисой параболы).

y²=2px − каноническое уравнение параболы.