Преобразования координат
Теорема. Если в декартовой системе координат задано уравнение 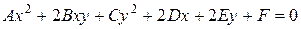 , (*)
, (*)
то существует такая декартовая система координат, в которой это уравнение приобретает один из следующих канонических видов:
1. 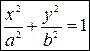 − эллипс,
− эллипс,
2. 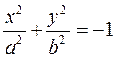 − мнимый эллипс,
− мнимый эллипс,
3. 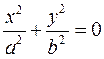 − пара мнимых пересекающихся прямых,
− пара мнимых пересекающихся прямых,
4. 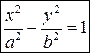 − гипербола
− гипербола
5. 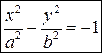 − сопряженная гипербола,
− сопряженная гипербола,
6. 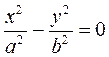 − пара пересекающихся прямых,
− пара пересекающихся прямых,
7. 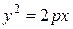 − парабола,
− парабола,
8. 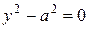 − пара параллельных прямых ( или совпавших при а=0),
− пара параллельных прямых ( или совпавших при а=0),
9. 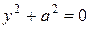 − пара мнимых параллельных прямых.
− пара мнимых параллельных прямых.
К каноническому виду уравнение (*) можно привести различными способами.
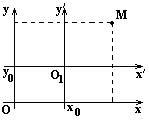
Параллельный перенос.
|
Если в уравнении (*) коэффициент 2В=0, то к каноническому виду уравнение приводится параллельным переносом осей координат по формулам:
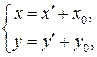 (1)
(1) 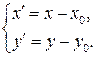 (2)
(2)
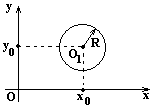
Уравнения кривых второго порядка, когда их центры симметрии находятся в точке с координатами O1(x0,y0), получаются с помощью преобразования координат при параллельном переносе осей (2):
|
1. 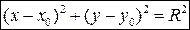 - уравнение окружности с центром в точке O1(x0,y0) и радиусом R;
- уравнение окружности с центром в точке O1(x0,y0) и радиусом R;
2. 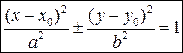 - уравнения эллипса и гиперболы с центром симметрии в точке O1(x0,y0);
- уравнения эллипса и гиперболы с центром симметрии в точке O1(x0,y0);
3. 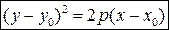 - уравнение параболы с вершиной в точке O1(x0,y0).
- уравнение параболы с вершиной в точке O1(x0,y0).
Поворот координатных осей
Если в уравнении (*) коэффициент 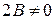 , то к каноническому виду уравнение приводится поворотом осей координат по формулам:
, то к каноническому виду уравнение приводится поворотом осей координат по формулам:
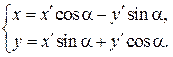 (3)
(3)
Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x¢,y¢) этой же точки при повороте осей на угол a.
Угол α может быть найден по формуле:
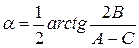 . (4)
. (4)
Если А=С то угол α принимают равным π/4.
Пример. Приведите уравнение 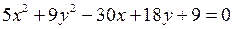 к каноническому виду и постройте кривую.
к каноническому виду и постройте кривую.
Выделим полный квадрат: сгруппируем члены этого уравнения, содержащие одноименные координаты:
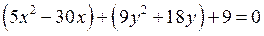 ,
, 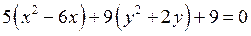 .
.
Дополним члены в скобках до полных квадратов:
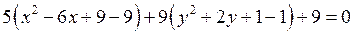 ,
, 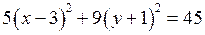 .
.
Введем новые координаты: 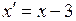 ,
, 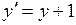 ,
, 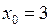 ,
, 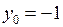 ,
,
то есть точка 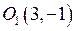 – центр кривой.
– центр кривой.
Уравнение в новой системе координат принимает вид:
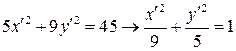 , определяет эллипс с полуосями
, определяет эллипс с полуосями 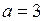 ,
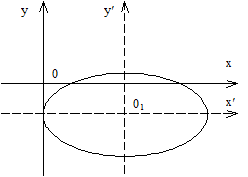
, 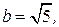 который в исходной системе координат имеет центр в точке
который в исходной системе координат имеет центр в точке 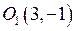 .
.
Пример. Определите вид кривой 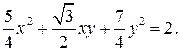
Определим угол поворота осей по формуле (4):
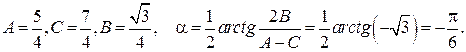
Подвергнем уравнение кривой преобразованию:
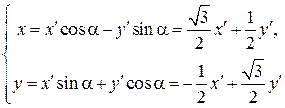
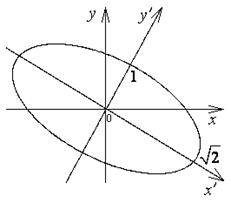
и получим уравнение эллипса
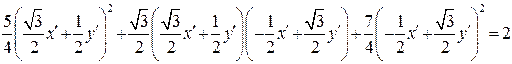 .
.
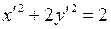 ,
, 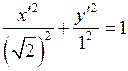 .
.
с полуосями 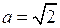 ,
, 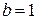 .
.
Дата добавления: 2020-03-17; просмотров: 525;











