Середньовагове, його вага та середньоквадратична помилка.
Найімовірніше значення величини, що його дістали з ряду нерівноточних результатів, називають середньоваговим значенням. Порядок його підрахунку видно з такого прикладу.
У групі 25 учнів з різним віком: 16 років—3, 17 років—6, 18 років—7, 19 років—6, 20 років— 3 чоловіка. Середній вік учнів становить:
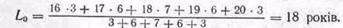
При розв'язанні загальний сумарний вік учнів поділено на загальне їх число. Число учнів кожного віку визначає значення, вагу цього віку в загальній масі учнів. Позначивши вік учнів через l1, l2,... lп а число учнів даного віку p1, p2, ... рп, можна записати:
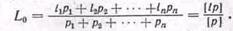
Це і є формула середньовагового значення. В ній l1, l2,... lп окремі результати вимірювань з вагами p1, p2, ... рп., або можна записати так:
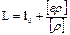
Середньоквадратична похибка арифметичної середини.
Вага арифметичної середини Р дорівнює сумі ваг рівноточних результатів вимірювань, за якими її обчислено:
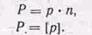
Вагу загальної арифметичної середини обчислюють також за формулою (60); вона дорівнює сумі ваг нерівноточних результатів вимірювань, за якими обчислено загальне арифметичне середнє.
Для обчислення середньої квадратичної помилки загальної арифметичної середини використовуємо формулу:
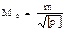
Для істинної помилки формула буде виглядати так:
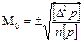
Для вірогідніших помилок формула буде такою:
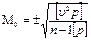
Дата добавления: 2020-03-17; просмотров: 717;











