Оцінка точності вимірювань. Оцінка точності вимірювань по нев'язках у полігонах і ходах.

Якщо б можна було кожний раз знати істинну похибку результату вимірювання, то вона була б тим єдиним та універсальним кількісним критерієм точності, що задовольняв би усі вимоги як теорії, так і практики. Оскільки найчастіше істинні похибки невідомі, то точність окремого вимірювання характеризується кількісним критерієм точності, що виражає умови вимірювань.

Для характеристики умов вимірювань в геодезичній практиці використовують середню квадратичну похибку.

Оскільки середня квадратична похибка m і гранична помилка 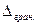характеризують умови вимірювань, то між ними повинна існувати деяка залежність. Якщо цю залежність виразити через рівняння:

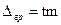
де t – деяка стала, то відшукування 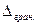зведеться до встановлення параметра t.

Довголітня практика геодезичних вимірювань показала, що параметр t в залежності від задачі, що вирішується, потрібно приймати 2 або 3. Тому граничну випадкову помилку вимірювання приймають

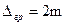
або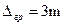

Виконуючи багаторазові вимірювання однієї ж величини, потрібно бути впевненим, в тому, що серед результатів нема таких, які містять грубі похибки. Для цього встановлюють допуски відхилень результатів вимірювань одне від одного, яким є визначення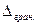

Для ряду рівноточних вимірювань однієї величини, граничне допустиме значення d _доп буде визначатися за формулою:

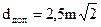
Правильність встановлення допусків має велике практичне значення, тому у приведених вище формулах слід використовувати надійні величини середніх квадратичних похибок безпосередніх вимірювань. Вони можуть бути отримані тільки на основі різноманітного виробничого матеріалу та відповідної його математичної обробки.

Досвід виконання геодезичних вимірювань відображається у нормативних документах (інструкціях, рекомендаціях, ДСТ), де вказують допуски, не тільки розраховані за формулами, але й всебічно перевірені практикою. Вони є головним критерієм якості геодезичних вимірювань і їх дотримання обов’язкове.