Вычисление производных
Вычисление сумм рядов
Для вычисляемой и инертной форм вычисления сумм служат функции:
| Вычисляемая форма: | Инертная форма: |
| sum(f,k) | Sum(f,k) |
| sum(f,k=m..n) | Sum(f,k=m..n) |
где f – функция, задающая члены суммируемого ряда,
k – индекс суммирования,
m и n – целочисленные пределы изменения k.
Значение n может приниматься бесконечным, тогда для n используется константа infinity.
Инертная форма начинается с большой буквы и служит для воспроизведения заданного выражения.
Примеры:
>Sum(k^2, k=1..5)=sum(k^2, k=1..5);
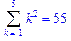
>sum(k^2,k);

>Sum(1/n!,n=1..infinity)=sum(1/n!,n=1..infinity);
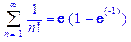
Вычисление произведений
Для вычисления произведений используются функции:
| Вычисляемая форма: | Инертная форма: |
| product(f,k) | Product(f,k) |
| product(f,k=m..n) | Product(f,k=m..n) |
Примеры:
>Product(k^2, k=1..5)=product(k^2, k=1..5);
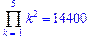
>product(k^2,k);
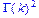
>Product(1/n!,n=1..infinity)=
product(1/n!,n=1..infinity);
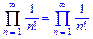
Вычисление производных
Для вычисления производных используются следующие функции:
| Вычисляемая форма: | Инертная форма: |
| diff(f,x1,x2,…,xn) | Diff(f,x1,x2,…,xn) |
| diff(f,[x1,x2,…,xn]) | Diff(f,[x1,x2,…,xn]) |
где f – дифференцируемое алгебраическое выражение, в частности функция f(x1,x2,…,xn) n переменных, по которым производится дифференцирование.
Первая из этих функций вычисляет в простейшем случае diff(f(x),x) первую производную функции f(x) по переменной x. При n>1 вычисления производных выполняются рекурсивно, т.е. diff(f(x),x,y) эквивалентно diff(diff(f(x),x),y). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff(f(x),x$4) вычисляет производную 4-го порядка и эквивалентно записи diff(f(x),x,x,x,x). А diff(g(x,y),x$2, y$3) эквивалентно diff(g(x,y),x,x,y,y,y).
Примеры:
>Diff(sin(x),x)=diff(sin(x),x);
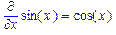
>Diff(x^3+y^2,x,y)=diff(x^3+y^2,x,y);
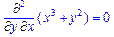
>Diff(x^6/6!,x$6)=diff(x^6/6!,x$6);
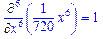
>diff([sin(x),x^n,exp(a*x)],x);
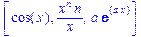
>simplify(%);
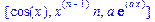
>f(x,y):=cos(x)*y^3;
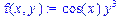
>Diff(f(x,y),x)=diff(f(x,y),x);
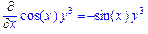
>Diff(f(x,y),x,y)=diff(f(x,y),x,y);
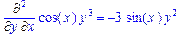
>Diff(f(x,y),[x,y])=diff(f(x,y),[x,y]);
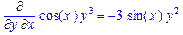
>Diff(f(x,y),x$4)=diff(f(x,y),x$4);
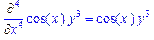
>Diff(f(x,y),x$3,y$2)=diff(f(x,y),x$3,y$2);
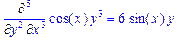
Для вычисления производных может использоваться дифференциальный оператор D. Он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор может записываться в формах:
D(f) или D[i](f)
где f – выражение или функция,
i – положительное целое число, выражение или последовательность.
Оператор D(f) вычисляет имя производной от f. В форме D(f)(x) этот оператор подобен diff(f(x),x).
>D(sin);
cos
>D(sin)(x)=diff(sin)x,x);
cos(x)=cos(x)
>D(sin)(Pi);
-1
Если f – функция n аргументов, то D[i](f) вычисляет частную производную по отношению к i-му аргументу. В общем случае D[i,j](f) эквивалентно D[i](D[j](f)) и D[](f)=f.
>fun:=(x)->sin(x^2);
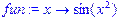
>D(fun);
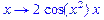
>diff(fun(x),x);
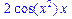
>f:=(x,y,z)->x*exp(y)+ln(z);

>D[1](f);

>D[2](f);
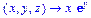
>D[3](f);
Дата добавления: 2020-10-01; просмотров: 534;











