Графический способ решения ЗЛП
Графический способ решения применим к ЗЛП в следующей постанвке: 1) целевая функция f→max(min); 2) ограничения должны быть записаны в виде неравенств, не обязательно одного знака; 3) число переменных n≤3.
Для простоты изложения рассмотрим случай n=2.
Выясним геометрический смысл неравенств, их решений и решений систем неравенств, то есть геометрический смысл системы ограничений.
Доказана теорема: множество решений неравенства с двумя переменными
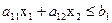
является одной из двух полуплоскостей, на которые вся плоскость делится прямой
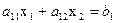 ,
,
включая и эту прямую, а другая половина плоскости с той же прямой есть множество решений неравенства
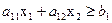
Пример. Построить множество решений неравенства:
а) 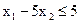 , б)
, б) 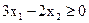 .
.
Решение. В соответствии с теоремой множество решений неравенства есть полуплоскость.
а) Построим границу полуплоскости – прямую 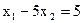 , найдя точки её пересечения с осями координат A(5,0) и B(0,-1) (рис.1).
, найдя точки её пересечения с осями координат A(5,0) и B(0,-1) (рис.1).
Для определения искомой полуплоскости (верхней или нижней) рекомендуется задать произвольную контрольную точку, не лежащую на её границе – построенной прямой. Если неравенство выполняется в контрольной точке, то оно выполняется во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости. И наоборот, в случае невыполнения неравенства в контрольной точке оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости. 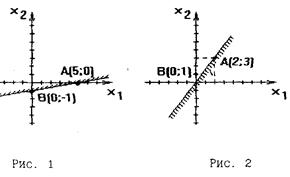
В качестве контрольной точки удобно взять начало координат
0(0,0), не лежащее на построенной прямой. Координаты точки 0
удовлетворяют неравенству 1*0-5*0≤5. Это неравенство - верное. Следовательно. решением данного неравенства является полуплоскость, содержащая точку 0. Искомая полуплоскость выделена штриховкой.
б)Построим границу полуплоскости — прямую 3х1-2х2=0 по двум точкам (рис. 2). Одной из этих точек является начало коорди-
нат, другую точку берем на прямой произвольно, например, А(2,3). В качестве контрольной точки здесь брать "самую простую" 0(0,0)
не следует, так как она лежит на прямой. Возьмем, например, точку
В(0.1). Так как координаты контрольной точки не удовлетворяют неравенству, т.е. неравенство 3*0-2*1≥0 не является верным, то решением данного неравенства является полуплоскость, не содержащая точку В(0,1). Искомая полуплоскость выделена штриховкой. Доказана теорема: множество решений совместной системы линейных неравенств с двумя переменными является выпуклым многоугольником (или выпуклой многоугольной областью).
Пример, Построить множество решений системы неравенств
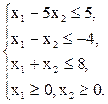
Для каждой прямой (границы полуплоскости) находим точки пересечения с осями координат и определяем соответствующую полуплоскость:
| 1) х1–5x2 =5, |
| 1*0 - 5*0 ≤ 5, 0<5; | ||||||
| 2) х1–x2<-4, |
| 1*0 –1*0 ≥ -4 0>-4; | ||||||
| 3) х1+х2<8 |
| 1*0+1*0 <8. |
Множеством всех решений системы неравенств – пересечение соответствующих полуплоскостей – треугольник АВС (рис. 3).
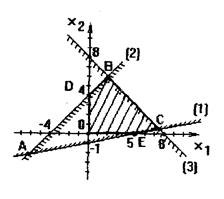
(рис. 3 )
Если учесть условия неотрицательности
х1 >о; х2>0,
то областью допустимых решений будет та часть треугольника АВС, которая находится в первой четверти, т.е. ОДВСЕ — многоугольник
допустимых решений, в дальнейшем — многоугольник решений.
При построении многоугольника решений возможны следующие частные случаи: многоугольная область (рис. 4); прямая линия (рис. 5): точка (рис. 6); множество. не содержащее допустимых решений (рис. 7); пустое множество, если система ограничений несовместна (рис. 8).

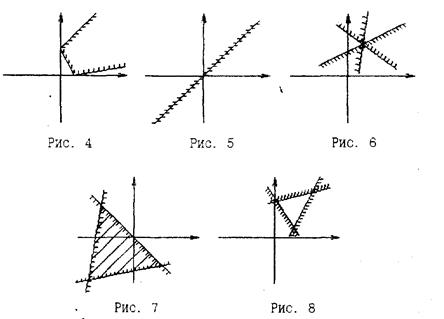

Итак, в общем случае множество всех допустимых решений системы ограничений ЗЛП при n = 2 — многоугольник решений — является выпуклым многоугольником (рис. З) или, в частности, выпуклой многоугольной областью (рис. 4).
Ответ на вопрос. В какой точке многоугольника решений возможно оптимальное решение ЗЛП, дается следующей Фундаментальной
теоремой: если ЗЛП имеет единственное оптимальное решение, то линейная функция принимает максимальное (минимальное) значение в одной из угловых точек многоугольника решений. Если линейная Функция принимает максимальное (минимальное) значение более чем в одной угловой точке. то она принимает его в бесчисленном множестве точек, являющихся отрезком — частью границы многоугольника решений.
Рассмотрим целевую функцию F(х1,х2)= с1х1+с2х2. Она является линейной функцией двух переменных х1, х2. В математическом анализе функций нескольких переменных вводятся понятия линии уровня функции нескольких переменных и градиента функции нескольких переменных.
Линией уровня функции двух переменных называется множество точек плоскости, в которых функция сохраняет одно и то же значение, т. е. f(х1, х2)= d или
f(х1,x2)= с1х1+ с2х2=d, d=const.
Линии уровня широко используются, например, на картах прогноза погоды (изотермы). Еще более простым примером линий уровня являются параллели на географической карте. Это линии уровня широты.
Градиентом функции 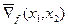 является вектор, который можно вычислить по формуле
является вектор, который можно вычислить по формуле
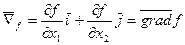
Он обладает следующими свойствами:
1) 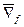 перпендикулярен линиям уровня функции
перпендикулярен линиям уровня функции 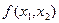 ;
;
2) 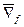 показывает направление наискорейшего возрастания функции
показывает направление наискорейшего возрастания функции 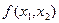 .
.
Если функция 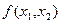 — линейная функция, то ее линии уровня образуют семейство параллельных прямых, а вектором-градиентом является вектор
— линейная функция, то ее линии уровня образуют семейство параллельных прямых, а вектором-градиентом является вектор
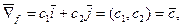
перпендикулярный линиям уровня.
Важное свойство линий уровня линейной функции в том, что при параллельном смещении линии в направлении вектора 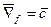 уровень только возрастает, а в направлении вектора
уровень только возрастает, а в направлении вектора 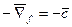 только убывает.
только убывает.
Используя все вышеизложенное, сформулируем порядок решения ЗЛП графическим способом.
1. 3аписать задачу в следующей форме: Г - шах или . - т г.,
ограничения-неравенства любого знака, число переменных п с 3.
2. Построить многоугольник решений.
3. Из начала координат построить вектор 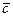 и провести через начало координат линию уровня целевой функции, перпендикулярно вектору
и провести через начало координат линию уровня целевой функции, перпендикулярно вектору 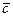 . Переместить линию уровня параллельно самой себе в направлении вектора
. Переместить линию уровня параллельно самой себе в направлении вектора 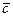 , если требуется определить максимум целевой функции, и в направлении вектора -
, если требуется определить максимум целевой функции, и в направлении вектора - 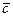 , если требуется определить минимум функции. В результате этого находим точку (точки).В которой целевая функция принимает максимальное (минимальное) значение, или устанавливаем неограниченность сверху (снизу) целевой
, если требуется определить минимум функции. В результате этого находим точку (точки).В которой целевая функция принимает максимальное (минимальное) значение, или устанавливаем неограниченность сверху (снизу) целевой
функции на множестве решений.
4. Решив соответствующую систему уравнений, найти координаты оптимального решения (плана).
5. Вычислить максимальное (минимальное) значение целевой функции и записать ответ.
Пример. Решить графически: f = -2x1 – 3x2 → min,
при ограничениях
x1 – 5x2 ≤ 5,
x1 – x2 ≥ -4,
x1 + x2 ≤8,
x1 ≥ 0, x2 ≥ 0.
Решение.
1. Задача поставлена в симметричной форме.
2. Многоугольник решений представлен на рис. 3.
3. Восстановим рис. 3 и из начала координат построим вектор c (-2, -3). Перпендикулярно ему проведём линию уровня, проходящую через начало координат. Перемещаем линию уровня в направлении вектора –с до тех пор, пока она имеет общие точки с многоугольником решений. Минимальное значение целевая функция принимает в точке B.
4. найдём координаты точки B. Для этого решим систему линейных алгебраических уравнений:
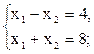
| 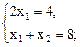
| 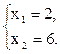
|
5. Вычислим значение целевой функции при x1=2, x2=6:
f=-2*2-3*6=-22
Ответ: fmin=-22, xопт=(2,6).
Рисунок, иллюстрирующий решение задачи:
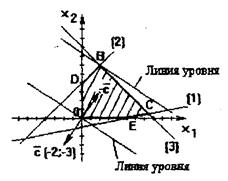
рис. 9
Частный случай 1. Решить графически задачу:
f=x1+x2→max;
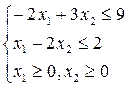
Решение
| 1) –2x1+3x2=9, |
| 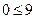
| ||||||
| 2) x1-2x2=2, |
| 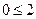
|
Рисунок, иллюстрирующий решение задачи:
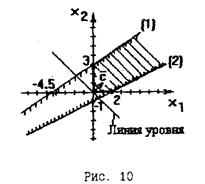
Многоугольник решений – многоугольная выпуклая область. Оптимальных решений нет, fmax→~.
Ответ: fmax→~; оптимальных решений нет.
Частный случай 2. Решить графически задачу:
F=x1-x2→max;
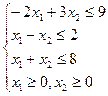
Решение
| 1) –2x1+3x2=9 |
| 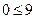
| ||||||
| 2) x1-x2=2 |
| 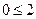
| ||||||
| 3)x1+x2=8 |
| 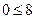
|
Рисунок, иллюстрирующий решение задачи:
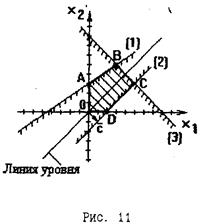
Если передвигать линию уровня, то она выйдет из области решений не в одной точке, как это было в основном примере, а сольется с прямой СД, которая является граничной линией области решений. В этом случае условимся говорить, что имеет место альтернативное решение, и с ответе указывать координаты точек С и Д.
Координаты точки С находим, решая систему:
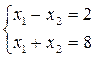
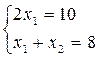
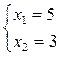
Координаты точки Д находим, решая систему:
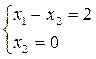
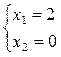 Д(2,0)
Д(2,0)
Значение целевой функции
f(C)=5-3=2; f(Д)=2-0=2; fmax=f(C)=f(Д)
Ответ:
fmax=2, 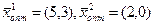
Пример. Решить графически:
f=9x1+3x2-5x3+5x4→max;
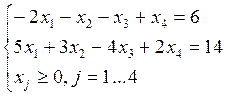
Решить пример самостоятельно.
Ответ: fmax=2, xопт=(2,0,0,2)
Дата добавления: 2020-02-05; просмотров: 687;











