Общая формулировка ЗЛП. Основные определения.
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Предметом математического программирования является разработка методов отыскания экстремального – максимального или минимального – значения функции нескольких переменных при конечном числе дополнительных ограничений, наложенных на эти переменные.
В общем виде математическая постановка задачи математического программирования (ЗПМ) такова: среди всех решений системы ограничений (2)
Найти то или те, которые доставляют максимум или минимум функции (1).
f(x1,x2, . . .,xn) → max (min), (1).
gi(x1,x2, . . .,xn)<= bi(>=bi), (2)
где f и gi - заданные функции, а bi – заданные действительные числа, i = 1…m.
В зависимости от свойств функций f и gi математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.
Если все функции f и gi линейные, то соответствующая задача является задачей линейного программирования (ЗЛП). Для решения ЗЛП разработан целый ряд эффективных методов, алгоритмов и программ.
ОБЩАЯ ПОСТАНОВКА ЗЛП
Математическая модель
В настоящее время в литературе насчитывается несколько де-
сятков определений понятия модель. Мы под моделью будем понимать условный образ какого-либо объекта. приближенно воссоздающий этот объект с помощью некоторого языка. Математические модели относятся к классу идеальных знаковых моделей и могут создаваться из любых математических объектов: чисел. функций, уравнений, графиков, графов и т.д., то есть представляют объект в абстрактном виде с помощью математических соотношений.
В математических моделях объектом является некий процесс (например, использование ресурсов, транспортные перевозки и т.п.). Математическая модель — математическое описание исследуемого процесса или объекта. Принято выделять три основных этапа математического моделирования. Первый этап — постановка задачи-
выбор цели и задачи исследования. качественное описание объекта;
второй этап — построение математической модели, выбор или разработка методов исследования, выбор соответствующего пакета прикладных программ или написание данной программы для компьютера,подготовка исходной информации. проверка пригодности построенной модели; третий этап — проведение численных экспериментов, обработка и анализ полученных, решений. интерпретация результатов, отбор наиболее оптимальных вариантов.
Примеры ЗЛП
Задача 1 — об использовании ресурсов. Из сырья двух видов:
S1 и S2, запасы которого ограничены и составляют соответственно
b1 и b2, единиц. изготавливается продукция трех видов: Р1, Р2 и
Р3. Известно количество единиц сырья каждого вида, необходимое для производства единицы каждого вида продукции. Введем обозначение aij –количества единиц i – го вида сырья, необходимое для производства единицы продукции pj , где i = 1, 2; j = 1, 2, 3. известен доход от реализации единицы каждого вида продукции – cj j = 1, 2, 3.
Требуется составить такой план производства продукции, чтобы предприятие получило от реализации всей продукции наибольший суммарный доход. Составить математическую модель задачи.
Полезно для понимания смысла задачи поместить данные в таблицу (табл.1).
Таблица 1
| Вид ресурса | Число единиц ресурса, затрачиваемых на изготовление единицы продукции | Запас ресурсов | ||
| P1 | P2 | P3 | ||
| S1 | a11 | a12 | a13 | b1 |
| S2 | a21 | a22 | a23 | b2 |
| Прибыль от единицы | c1 | c2 | c3 |
Решение.
1. Выберем переменные. Пусть xj -число единиц продукции вида Pj , запланированное к производству, j = 1, 2, 3.
2. Очевидно, xj >=0. (1)
3. Цель – получение наибольшей суммарной прибыли. Суммарная прибыль f составит сумму c1x1 денежных единиц от реализации запланированной продукции P1 , c2x2 –от продукции P2, c3x3 – от продукции P3, т.е.
f= c1x1+c2x2+c3x3 → max… (2)
4. Для изготовления запланированного объема продукции потребуется (a11x1+a12x2+a13x3) единиц ресурса S1 для S2 – аналогично. Так как потребление ресурсов не должно превышать их запасов, соответственно b1 и b2 , то связь между потреблением ресурсов и их запасами выразится системой неравенств:
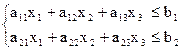 (3)
(3)
Постановка математической задачи: среди всех неотрицательных решений системы неравенств (3) найти то или те, при которых функция (2) принимает максимальное значение.
Так как функция (2) линейная, асистема (3) содержит только линейные неравенства, то задача (1) – (3) является задачей линейного программарования.
Задача 2. Транспортная задача (ТЗ) по критерию стоимости.
Пусть имеются два пункта отправления А1 и А2, в которых сосредоточено соответственно а1,а2 единиц однородного груза. Весь этот груз следует перевезти в три пункта назначения: В1, В2, В3. Причем потребности пунктов назначения известны и составляют соответственно b1,b2,b3 единиц этого груза. Стоимость перевозки единицы груза из каждого пункта отправления Аi в каждый пункт назначения Bj известно; обозначим её cij - денежных единиц.
Замечание. В задаче предполагается, что суммарный запас груза в пунктах отправления равен суммарным потребностям пунктов, т.е. выполняется равенство:
а1+а2=b1+b2+b3 (4)
Решение.
1. Выберем переменные. Пусть xij - количество единиц груза, предназначенного для перевозки из пункта отправления А1 в пункт назначения Вj; i = 1,2; j = 1,2,3.
2. Очевидно ,
xij>=0, i=1,2, j= 1,2,3. (5)
Таблица 2
| Пункты отправления | Стоимость перевозки единицы груза в пункты назначения | Запасы груза | ||
| B1 | B2 | B3 | ||
| A1 | c11 | c12 | c13 | a1 |
| A2 | c21 | c22 | c23 | a2 |
| Потребности в грузе | b1 | b2 | b3 |  a1= a1=  b1 b1
|
3. Цель – минимальная суммарная стоимость перевозок. Суммарная стоимость перевозок f складывается из стоимостей перевозок всех запланированных объемов. Так, если из пункта А1 в пункт В1 следует перевезти х11 единиц груза, причем стоимость перевозки единицы груза с11 денежных единиц, то оказанная перевозка оценивается в с11х11 денежных единиц. Суммируя, получаем:
f=c11x11+c12x12+c13x13+c21x21+c22x22+c23x23. (6)
4. Поскольку весь груз следует перевести, то получаем систему уравнений:
х11+х12+х13 = а1
х21+х22+х23 = а2. (7)
Систему уравнений (7) называют ограничениями по запасам.
Поскольку все потребности следует удовлетворить, то получаем систему уравнений:
х11+х21 = b1
х12+х22 = b2 (8)
х13+х23 = b3
Систему уравнений (8) называют ограничениями по потребностям.
Постановка математической задачи: среди всех неотрицательных решений системы уравнений (7), (8) найти то или те, при которых функция (6) достигает минимума.
Задача 3. – задача о смесях. При откорме животных каждое животное ежедневно должно получать не менее 60 ед. питательного вещества А, не менее 50 ед. питательного вещества В и не менее 12 ед. питательного вещества С. Указанные питательные вещества содержат три вида корма. Содержание единиц питательных веществ в одном кг каждого из видов корма приведено в следующей таблице.
Таблица 3
| Питательные вещества | Количество ед. питательных веществ в 1 кг корма | ||
| 1 вида | 2 вида | 3 вида | |
| А | |||
| В | |||
| С |
Составить дневной рацион, обеспечивающий получение необходимого количества питательных веществ при минимальных денежных затратах, если цена 1 кг корма одного вида составляет 9 денежных единиц, корма 2 вида – 12 денежных единиц и корма 3 вида – 10 денежных единиц. Составить математическую модель.
Решить задачу самостоятельно.
Ответ: f = 9x1+12x2+4x3→ min;
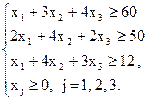
Общая формулировка ЗЛП. Основные определения.
Определение. Общей ЗЛП называется задача, которая состоит в определении максимального или минимального значения функции
f= 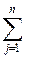 cjxj → max(min) (1)
cjxj → max(min) (1)
при условиях
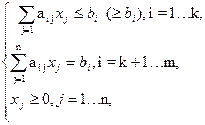
| (2) |
| (3) |
где ai j , bi , cj - заданные постоянные величины и k≤m.
Определение. Стандартной или симметричной ЗЛП называется задача, которая состоит в определении максимального (минимального) значения функции
f= 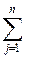 сjxj → min (max) (4)
сjxj → min (max) (4)
при условиях
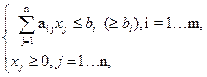
| (5) |
| (6) |
Определение. Основной или канонической ЗЛП называется задача, которая состоит в определении минимального значения функции
f = c1x1+c2x2+…..cnxn → min (7)
и условиях
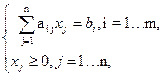
| (8) |
| (9) |
Определение. Функция (1), экстремум которой ищется, называется целевой функцией или функцией цели ЗЛП. Системы неравенств (2) , или уравнений (3) называются системами ограничения ЗЛП.
Определение. Совокупность чисел х = (х1,х2,….хn), удовлетворяющей системе ограничений (2), (3), называется допустимым решением или планом ЗЛП.
Определение. Совокупность всевозможных допустимых решений ЗЛП называется областью допустимых решений ЗЛП.
Определение. Допустимое решение задачи, при котором целевая функция принимает свое максимальное (минимальное) значение называется оптимальным решением или оптимальным планом ЗЛП.
Указанные выше 3 формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решений одной из указанных задач, то тем самым может быть определен оптимальный план любой из 3 задач.
Чтобы перейти от одной формы записи ЗЛП к другой, нужно в общем случае уметь, во-первых, сводить задачу максимизации функции к задаче минимизации, во-вторых, переходить от ограничений – неравенств к ограничениям – равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.
В том случае, когда требуется найти максимум функции
f = c1x1+с2x2+…+сnxn →max, (19)
можно перейти к нахождению минимума функции
f = -f = - c1x1-c2x2-…..-cnxn →min (20)
при этом
max(f)= - min (-f). (21)
Ограничения неравенства, имеющий вид «≤», можно преобразовать в ограничения-равенства добавлением к левой части дополнительной неотрицательной переменной. А ограничения-неравенства вида «≥» - в ограничение-равенство вычитанием из левой части дополнительной неотрицательной переменной. Эти дополнительные переменные называют балансовыми, и в конкретных задачах они имеют вполне определённый экономический смысл. Таким образом, ограничение-неравенство
a11x1+a12x2+…..+a1nxn ≤b1
преобразуется в ограничение-равенство
a11x1+a12x2+…..+a1nxn+xn+1 =b1, xn+1≥0,
а ограничение-неравенство
a11x1+a12x2+…..+a1nxn+xn+1 ≥b1-
в ограничение-равенство
a11x1+a12x2+…..+a1nxn-xn+1 =b1, xn+1≥0.
Пример. Преобразовать постановку данной задачи в каноническую:
f=-2x1+x2+5x3→max;
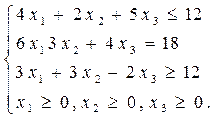
Решить пример самостоятельно.
Ответ:
f=2x1-x2-5x3→min;
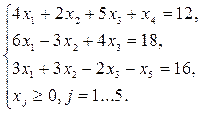
Для того, чтобы записать ограничения-равенства в виде ограничений-неравенств, необходимы сведения из линейной алгебры. Рассмотрим конкретный пример. Преобразовать постановку данной задачи в симметричную.
f=9x1+3x2-5x3+5x4→max;
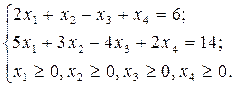
Дата добавления: 2020-02-05; просмотров: 661;











