Правила эквивалентных преобразований структурных схем: последовательное, параллельное соединение и обратная связь
Существует три основных типа соединения звеньев:
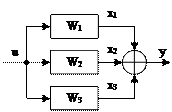
1 последовательное соединение (рисунок 3а);
2 согласно-параллельное соединение или сокращенно просто параллельное соединение (рисунок 3б);
3 встречно-параллельное соединение или сокращенно просто обратная связь (рисунок 3в).
| а | б | в |

| 
|
|
Рисунок – Типовые соединения звеньев
Рассмотрим подробно все виды соединений и способы нахождения эквивалентных передаточных функций таких соединений.
Последовательным называется такое соединение, когда сигнал с выхода одного звена подается на вход последующего.
При последовательном соединении передаточные функции отдельных звеньев перемножаются, и при преобразовании структурных схем цепочку из последовательно соединенных звеньев заменяют одним звеном с передаточной функцией:
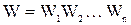 , (1)
, (1)
где n – число звеньев в цепочке.
Параллельным называется такое соединение, когда на вход звеньев подается один сигнал, а выходные сигналы звеньев складываются.
При параллельном соединении передаточные функции отдельных звеньев складываются, и при преобразовании структурных схем их заменяют одним звеном с передаточной функцией:
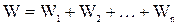 , (2)
, (2)
где n – число звеньев в цепочке.
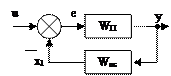
Звеном, охваченным обратной связью называется соединение двух звеньев, при котором выход звена прямой цепи подается на вход звена обратной связи, выход которого складывается с входом первого звена.
Если сигнал обратной связи складывается с отрицательным знаком, то обратная связь называется отрицательной, если с положительным – положительной. Если передаточная функция обратной связи равна единице ( 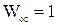 ), то обратная связь называется единичной, иначе – неединичной.
), то обратная связь называется единичной, иначе – неединичной.
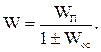 (3)
(3)
Докажем объявленные выше способы нахождения эквивалентных передаточных функций для типовых соединений, используя метод прогонки сигнала.
Составим систему уравнений для случая последовательного соединения звеньев:
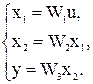
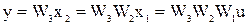 .
.
Тогда передаточная функция такого соединения из полученного уравнения находится как отношение выходного сигнала к входному:
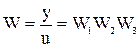 .
.
Составим систему уравнений для случая параллельного соединения:
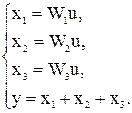
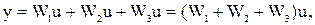
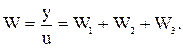
Составим систему уравнений для звена, охваченного обратной связью:
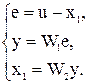
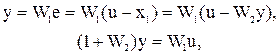
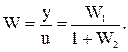
Дата добавления: 2020-02-05; просмотров: 1443;











