Последовательная схема

Задано дифференциальное уравнение, описывающее состояние системы:

.

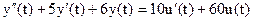Тогда передаточная функция для такой системы будет иметь вид:

.

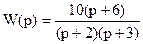Приведем передаточную функцию системы к виду последовательно соединенных звеньев первого порядка, т.е.

.

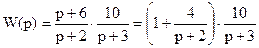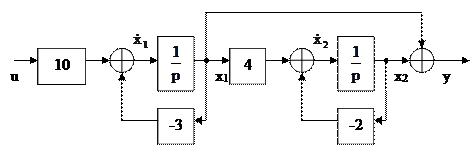
Структурная схема для такого вида передаточной функции имеет вид:

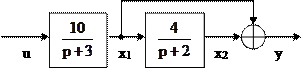
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:

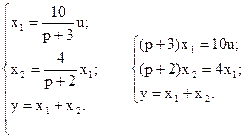
Учитывая, что p – это оператор дифференцирования, т.е. 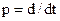, запишем

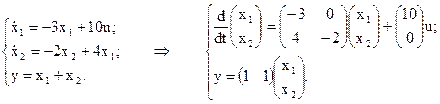
Тогда, принимая во внимание, что типовая форма записи метода пространства состояний имеет вид:

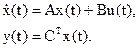
запишем матрицы A,B и C:

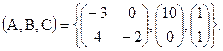
На основании полученных уравнений получим структурную схему для физической системы.

Структурная схема физической системы это структурная схема специфической конфигурации, состоящая из интеграторов, коэффициентов усиления и сумматоров. Данная структурная схема представляет собой заготовку для исследования системы с использованием компьютера.

Параллельная схема

Передаточная функция системы имеет вид:

.

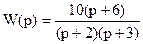Приведем передаточную функцию системы к виду параллельно соединенных звеньев первого порядка, т.е.:

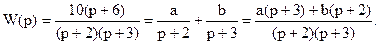
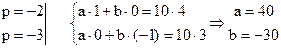
Тогда запишем следующее:

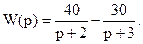
Структурная схема для такого вида передаточной функции имеет вид:

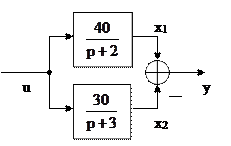
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:

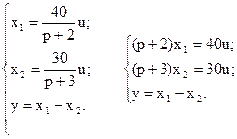
Учитывая, что p – это оператор дифференцирования, т.е. 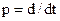, запишем:

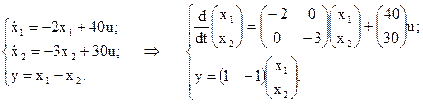
Запишем матрицы A,B и C:

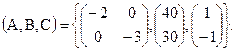
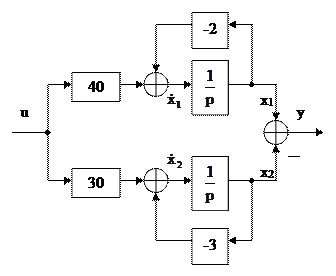
На основании полученных уравнений получим структурную схему для физической системы.

Нормальная схема

Передаточная функция системы имеет вид:

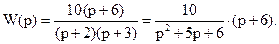
Структурная схема для такого вида передаточной функции имеет вид:

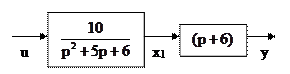
Составим систему уравнений по приведенной структурной схеме относительно выходных сигналов звеньев системы:

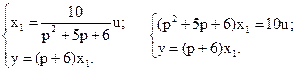
Учитывая, что p – это оператор дифференцирования, т.е. 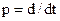, запишем:

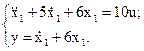
Учитывая то, что при использовании метода пространства состояний матричная форма записи системы дифференциальных уравнений составляется относительно ДУ первого порядка, понизим уравнение второго порядка относительно сигнала 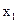, введя промежуточный сигнал 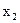так, что

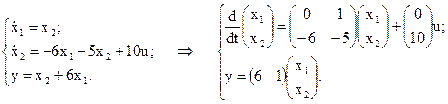
Запишем матрицы A,B и C:

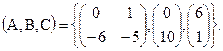
На основании полученных уравнений получим структурную схему для физической системы.

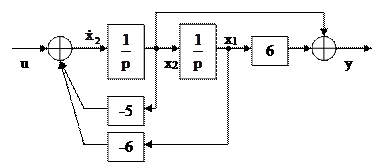
Таким образом, используя три основных схемы перехода можно перейти от формы представления системы в виде передаточной функции к форме пространства состояний.

Как уже было отмечено, существует и обратный путь перехода, т.е. от формы описания с помощью пространства состояния к операторной передаточной функции.

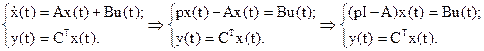
здесь 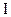- единичная матрица.

Тогда относительно выходного сигнала можно записать:

,

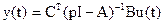а выражение для передаточной функции имеет вид:

,

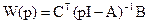здесь 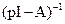- обратная матрица для матрицы *.

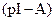Таким образом, зная матрицы A, B и C, можно найти выражение для операторной передаточной функции.