Частотные характеристики: способ получения, связь, показатели качества.

При рассмотрении частотных характеристик считаем, что на входе системы дейст­вует гармонический сигнал с амплитудой 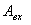и часто­той :

.

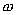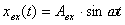По окончании переходного процесса на выходе линейной системы будут существовать гармонические колебания с той же частотой, что и у входного сигнала, но в общем случае отличающиеся от него по амплитуде и фазе, т.е. в установившемся режиме выходная величина звена равна:

,

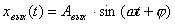где 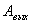– амплитуда установившихся выходных колебаний; 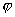– фазовый сдвиг между входными и выходными синусоидальными колебаниями.

При изменении частоты 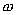изменяется, как соотношение между амплитудами входных и выходных колебаний, так и фазовый сдвиг 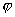между ними.

При этом зависимость от частоты отношения амплитуд называется амплитудно-частотной характеристикой (АЧХ), т.е.

.

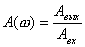Зависимость величины фазового сдвига от частоты 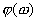называется фазо-частотной характеристикой (ФЧХ).

Частотная передаточная функция легко получается из обычной передаточной функции подстановкой 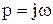, т.е.

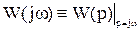(8)

Частотная передаточная функция 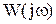представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в виде:

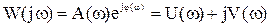, (9)

здесь

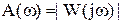– амплитудная частотная характеристика (АЧХ);

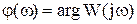– фазовая частотная характеристика (ФЧХ);

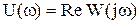– вещественная частотная характеристика (ВЧХ);

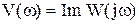– мнимая частотная характеристика (МЧХ).

На комплексной плоскости частотная передаточная функция определяет вектор, длина которого равна 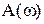, а аргумент равен углу 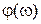, образованному этим вектором с положительной действительной полуосью. Годограф этого вектора, т.е. кривую, описываемую концом вектора 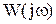при изменении частоты от 0 до ∞ или от -∞ до +∞, называют амплитудно-фазовой частотной характеристикой (АФХ) или годографом Найквиста.

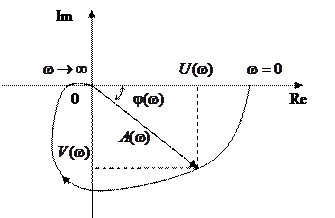
Рисунок - Амплитудно-фазовая частотная характеристика

Для нахождения вещественной и мнимой частей частотной передаточной функции часто бывает необходимо освободиться от мнимой части в ее знаменателе. Для этого следует ее числитель и знаменатель умножить на сопряженный знаменателю множитель. Например, если

,

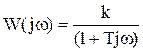то

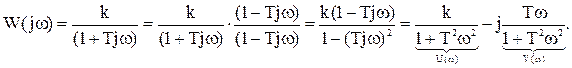
В общем случае амплитудная частотная характеристика имеет вид:

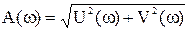, (10)

а фазовая частотная характеристика:

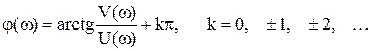(11)

При построении частотных характеристик систем, состоящих из нескольких соединенных типовых звеньев, удобно пользоваться следующими правилами вычисления модуля и аргумента комплексных функций [1]:

- модуль произведения 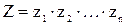комплексных чисел равен произведению модулей сомножителей:

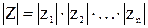, (12)

- а аргумент – сумме аргументов сомножителей:

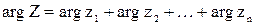. (13)

- модуль дроби комплексных чисел 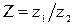равен дроби модулей:

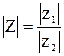, (14)

- а аргумент – разности аргументов числителя и знаменателя:

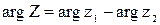. (15)

При исследовании систем управления амплитудную и фазовую характеристики удобно строить в логарифмических координатах. При этом построение точных графиков логарифмических функций даже типовых звеньев требует достаточно трудоемких вычислений, поэтому на практике удобно пользоваться приближенными асимптотическими логарифмическими характеристиками.

Прологарифмируем выражение (9):

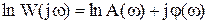. (16)

Из выражения (16) видно, что первое слагаемое определяет логарифмическую амплитудную частотную характеристику (ЛАЧХ), а второе – логарифмическую фазовую частотную характеристику (ЛФЧХ). ЛАЧХ строится в виде зависимости 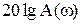от 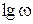, а ЛФЧХ в виде зависимости 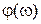от .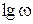

Использование логарифмических характеристик позволяет достаточно просто строить частотные характеристики системы, состоящей из нескольких звеньев, т.к. если прологарифмировать выражение (12) мы получим, что логарифм модуля произведения равен сумме логарифмов модулей сомножителей:

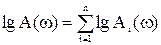. (17)

Фазовая частотная характеристика строится в логарифмическом масштабе только по оси абсцисс, т.е. фазовый сдвиг цепочки звеньев и так получается просто в виде суммы фазовых сдвигов на отдельных звеньях, что видно из выражения (13).

На оси частот обычно указывают либо значение 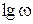, тогда единицей приращения является одна декада, либо значение самой частоты .

Интервал частот, отличающихся друг от друга в 10 раз называют декадой и обычно принимают за единицу логарифмического масштаба [2].

Как было отмечено ранее, для построения ЛАЧХ находится величина 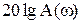, которая обозначается 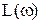и выражается в децибелах. Децибел равен одной десятой бела.

Бел – логарифмическая единица, которая соответствует десятикратному увеличению мощности, т.е. 1 бел соответствует усиления мощности в 10 раз, 2 бела – в 100 раз и т.д..

Проиллюстрируем порядок построения асимптотической ЛАЧХ на примере апериодического звена первого порядка с передаточной функцией:

.

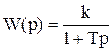Запишем частотную передаточную функцию звена:

.

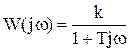Выделив реальную и мнимую части частотной передаточной функции, получим выражения для амплитудной и фазовой частотных характеристик:

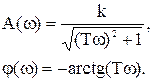
Прологарифмируем выражение для амплитудной частотной характеристики:

.

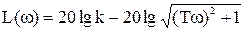Для простоты построения при 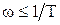пренебрегают слагаемым 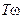под корнем, т.к. оно меньше единицы, а при 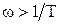- единицей. Тогда выражение для асимптотической ЛАЧХ апериодического звена можно записать в виде:

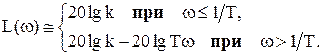
Частоты, на которых асимптотические ЛАЧХ претерпевают излом, называются сопрягающими частотами.

Для построения асимптотической ЛАЧХ системы с произвольной передаточной функцией необходимо предварительно записать ее в следующем виде:

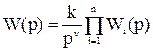, (18)

где 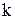- общий коэффициент усиления системы;

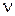- порядок астатизма системы, который определяется числом идеальных интегрирующих звеньев в системе;

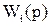- передаточная функция типового звена с единичным коэффициентом усиления, а 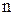- число типовых звеньев.

Правило построения асимптотических ЛАЧХ:

1. записать передаточную функцию системы в виде соединения типовых звеньев согласно выражению(18);
2. вычислить величину начального усиления равную ;
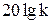3. определить все сопрягающие частоты и последовательно пронумеровать их;
4. отметить все сопрягающие частоты на оси абсцисс;
5. отметить точку ( 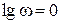; 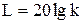) на координатной плоскости;
6. через отмеченную точку провести первую асимптоту под наклоном - 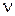20 дБ/дек до первой частоты сопряжения;
7. следующая асимптота проводится от конца первой асимптоты до следующей частоты сопряжения под наклоном 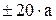дБ/дек, при этом a определяет порядок звена, а знак зависит от того, в числителе или знаменателе соответственно находится множитель, содержащий частоту спряжения на конце данной асимптоты.
8. таким образом строятся последующие асимптоты: i-тая асимптота начинается от сопрягающей частоты 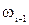до частоты 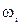, при этом наклон определяется частотой .

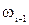Последняя асимптота представляет собой прямую, которая начинается от частоты 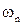и уходит в бесконечность, при этом ее наклон будет соответствовать выражению 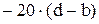дБ/дек, где d – порядок знаменателя передаточной функции, а b – порядок числителя. Конечный наклон асимптотической ЛАЧХ всегда будет отрицательный, что является следствием из правила физической реализуемости системы