Расчеты по точной теории
При расчетах по точной теории СК рассматривают как шарнирный четырехзвенник (рисунок 15).
Принимают, что кривошип ОА вращается вокруг точки О против часовой стрелки с постоянной угловой скоростью ω.
Тогда путь точки А:
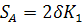 (51)
(51)
где 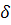 – угол размаха балансира;
– угол размаха балансира;
К1 – плечо балансира (длина дуги равна 2 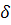 ).
).
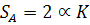 (52)
(52)
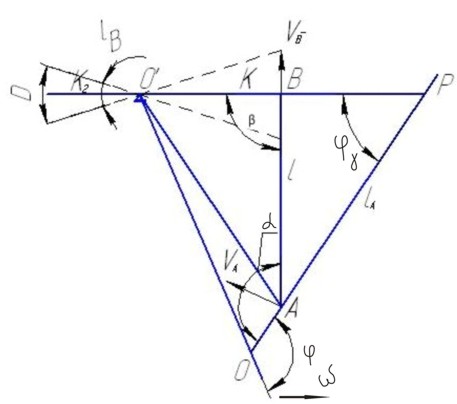
Рисунок 23- Схема к расчету СК по точной теории.
Линейная скорость точки А направлена перпендикулярно радиусу кривошипа и равна 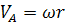 .
.
Скорость 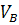 также перпендикулярна плечу балансира ОВ. Для определения скорости
также перпендикулярна плечу балансира ОВ. Для определения скорости 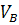 представим, что движение шатуна есть вращение в каждый момент вокруг некоторого мгновенного центра. Положение этого центра – точка Р находится на пересечении линий АР и ВР.
представим, что движение шатуна есть вращение в каждый момент вокруг некоторого мгновенного центра. Положение этого центра – точка Р находится на пересечении линий АР и ВР.
Согласно соотношению 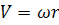 находим:
находим:
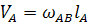 (53)
(53)
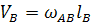 (54)
(54)
и тогда 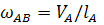 ,
, 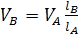 (55)
(55)
и по теореме синусов 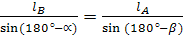
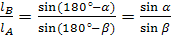 (56)
(56)
Если скорость точки А нам известна и равна ωr , то:
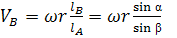 (57)
(57)
Это и есть скорость точки В по точной теории.
Ускорение точки В есть, как известно, производная от скорости:
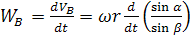 (58)
(58)
Для упрощения формулы (58) прибегают к таким рассуждениям.
Ускорение точек А и В можно разложить на тангенциальную (касательную) и нормальную составляющие.
Т.к. кривошип вращается с постоянной угловой скоростью, то касательное ускорение точки А равно 0.
Тогда, интересующее нас касательное ускорении точки В определяется по формуле:
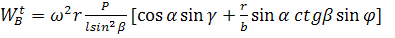 (59)
(59)
На рисунке 24 изображены ускорения, рассчитанные по элементарной (1), уточненной (2) и точной (3) теориям для СКН-10-2115.
Максимальное ускорение в начале хода вверх отклоняется от ускорения, определенного по элементарной теории в сторону увеличения на
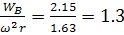 (на 30%)
(на 30%)
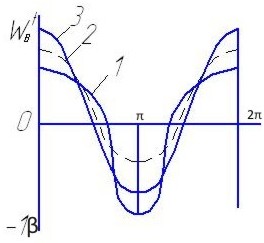
Рисунок 24- Графики ускорений, рассчитанные по элементарной (1), уточненной (2) и точной (3) теориям.
Дата добавления: 2016-06-18; просмотров: 1919;











