Расчеты по элементарной теории

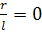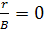При расчетах по элементарной теории принимается: а) точка движется не по дуге В₁ВВ₂, а по прямой В₁В₂ (рисунок 20); б) отношение и , т.е. радиус кривошипа настолько меньше шатуна и плеча балансира, что его отношение к этим величинам пренебрегается; в) угол ψ=0, т.е. шатун имеет бесконечную длину.

Результаты расчетов по элементарной теории можно с достаточным приближением применить для СК с малой длиной хода (до 4,5 м) и малым числом ходов. Рассматривая движение точки В₁, мы считаем его аналогичным движению точки подвеса штанг – точка Д.

Расчеты ведем в следующей последовательности.

Рисунок 20-Четырехзвенный механизм СК.

Находим путь, пройденный точкой В S_в при повороте кривошипа на угол 𝜑.

, (22)

но (23)

При верхнем положении шатуна ВО найдем опустив перпендикуляр из точки А на ВО получив треугольники АСО и АВС. Из ∆ АСО: ОС=r ,

из ∆ АВС: ВС= 𝑙 . Но ОС+ВС=ВО,

тогда ВО= r и S_В=ВВ₁=r+𝑙 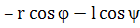(24)

т.к. ψ=0, то S_В=r(1- (25)

Угол поворота кривошипа =ω t, (26)

где ω – угловая скорость,

t – время поворота.

Тогда

S_В=r (1- (27)

Это и есть движении точки «В» по элементарной теории.

Скорость движения точки «В» определяют как первую производную пути по времени:

Имея ввиду, что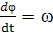

и g w:val="EN-US"/></w:rPr><m:t>П‰t</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

получим:

(29)

Ускорение точки «В» находят как вторую производную пути по времени или как первую производную скорости по времени

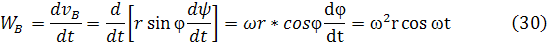
Рисунок 21- Графики пути, скорости и ускорения

Величину пути, скорости и ускорении для точки подвеса штанг (точка Д) можно определить, введя в полученные выше формулы соотношение плеч балансира К₁ и К.

(31)

(32)

(33)

Из формул видно, что скорость точки «Д» изменится по синусоиде, ускорение – косинусойде. Следовательно, их можно построить, если на оси абсцисс откладывать угол поворота кривошипа или время, пропорциональное этому углу, а по оси ординат- скорость или ускорение.